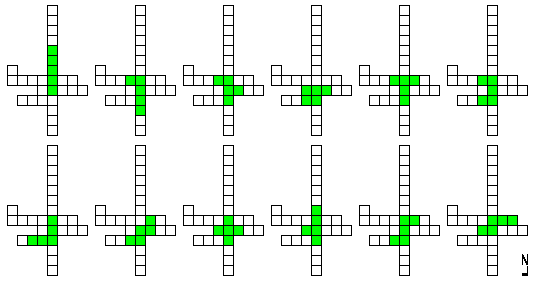
Deze vorm bestaat uit 27 vierkantjes.
Als je in deze vorm elke pentomino een strategische positie geeft (één tegelijk) dan is het onmogelijk om nog een tweede congruente pentomino binnen deze vorm te plaatsen.
We hebben een vorm van 31. George Sicherman breidde hem uit tot 34.
Wil je hem zien? Klik dan hier.
George Sicherman breidde Livio's vorm nog op andere manieren uit.
Wil je het zien klik dan hier.
Graag ontvangen we oplossingen. Je mag een totaal andere vorm maken
We kregen van Helmut Postl een vorm van 44.
Daan Juttmann brak dit record; hij heeft een vorm van 45. Proficiat!
Aad van de Wetering merkte op:" De oplossing van Daan heeft twee raakpunten, ik denk dat der Helmut die met opzet heeft vermeden."
Dit zou kunnen , maar in onze opgave staat nergens dat er geen raakpunten mogen zijn.
Ook George Sicherman mailde: "Helmut Postl's 44-cell solution to the Liviopuzzel can be extended by one cell. But Aad van de Wetering may veto this ex-tension."
George Sicherman brak het record van Daan:"Here is an even bigger solution to the Livio-puzzel: 47 cells."
Graag ontvangen we ook minder goeie oplossingen

Omdat Thinkquest de mooie tetrominosite van Casper verwijderd heeft publiceren we hier het gelijkaardig tetrominoprobleem
Carelli-puzzel
Dit leuke tetrominospel kregen we van onze mailvriend Livio Zucca uit Italië.
Zijn vriend Gabriele Carelli maakte deze leuke puzzel.
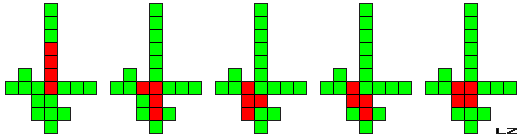
Deze vorm bestaat uit 20 vierkantjes.
Als je in deze vorm elke tetromino een strategische positie geeft (één tegelijk) dan is het onmogelijk om nog een tweede congruente tetromino binnen deze vorm te plaatsen.
David Clarke stuurde een oplossing van 27. Wil je hem zien? Klik dan hier.
Helmut Postl stuurde ook een oplossing van 27. Om de oplossing te zien klik hier
Graag ontvangen we oplossingen. Je mag een totaal andere vorm maken

Herdt-puzzel
Deze variatie van de Carelli-puzzel kregen we van Bryce Herdt.
"The further restriction I propose is that the large shape is capable of holding more than one of any pentomino.
To show you what I mean, here's a 20-square answer for the tetrominoes (may or may not be optimal)"
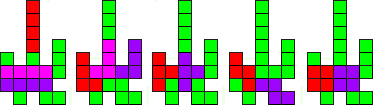
Je kan binnen de vorm meer dan één tetromino plaatsen.
"As with the original puzzle, each of the tetrominoes ILOST can be placed once in the shape so that no other copies can be placed. But it is also possible to place two or three copies of each tetromino in the shape without overlap".
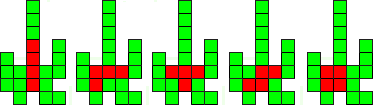
We kregen van George Sicherman een oplossing van 30 vierkantjes voor de pentomino's.
"This solution is an extension of Livio's solution to the original problem"
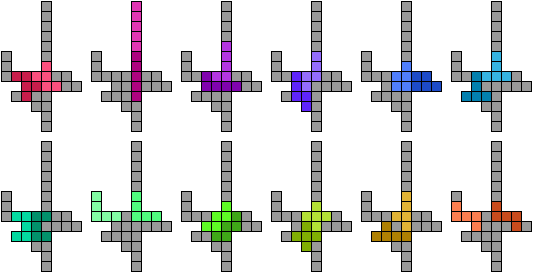
Bedankt George.
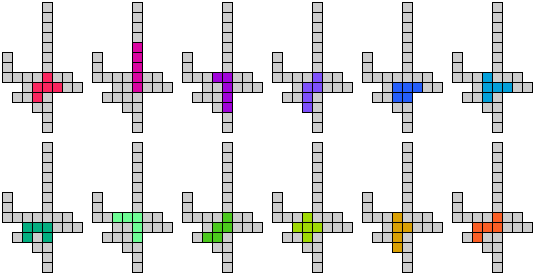
Graag ontvangen we nog andere oplossingen. Je mag een totaal andere vorm maken
