Pentominoes in 4 squares
 Alexandre Muņiz

We found this puzzle on facebook of Puzzle Fun
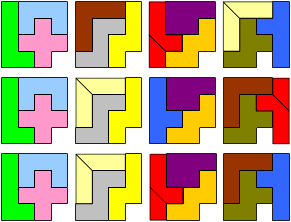
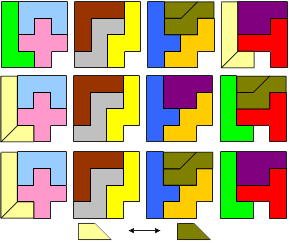
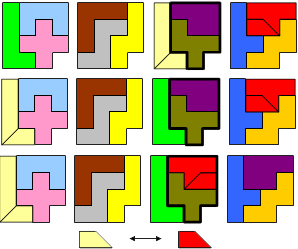
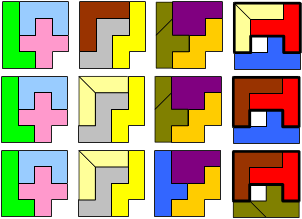
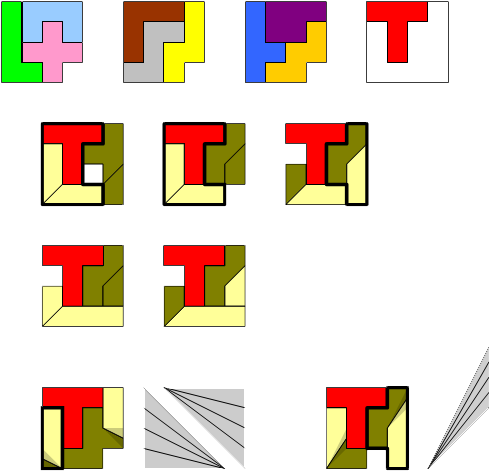
Start with the 12 pentominoes.

 Make a single diagonal cut in two of the pentominoes.
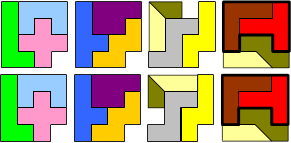
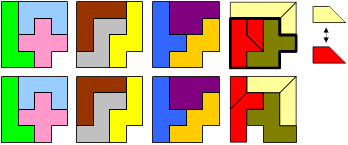
Pack the resulting 14 pieces and 4 monominoes into four 4×4 squares.

We got a wonderful document of Helmut Postl.
Since the I-pentomino is the only one which does not fit into a 4×4-square, it has to be split all the time. There seems to be no way to cut the I-pentomino twice, so the second cut has to be made on a different pentomino. For all given solutions, this is the F or the T.
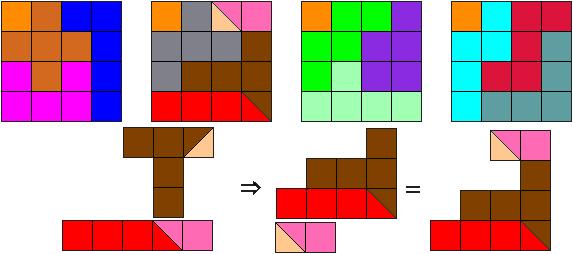
Remark: Only holes of polyomino shape are considered. There are many more possibilities if the holes may have diagonal borders. (This is an other nice problem)

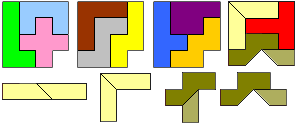
Two squares contain 3 whole pentominos, and two squares contain 2 whole pentominoes.
1. Each of the four squares contain exactly one monomino hole.
In the sequel, a thick black closed line is meant to surround a symmetric shape which can be flipped over to give new solutions.

In the following 12 solutions (resp. 18, if the swap of the two indicated small pieces of same shape are counted as different) each of the four holes is located at a corner. In the following 6 solutions (resp. 9 counting the swaps) three holes are at a corner, and one hole lies on the edge.

In this 3 solutions the I and T are cut

In this 3 (resp. 6) solutions the I and F are cut. 

In this 6 solutions the I and F are cut.

In this 6 (resp. 12) solutions the I and T are cut.

In the following 6 solutions three holes are at a corner, and one hole lies inside.
Here, the I and F are cut.

2. One square contains two monomino holes.
In the following 4 solutions the third square contains two holes, and the last square contains no hole.
Here, the I and F are cut.


 Three squares contain 3 whole pentominos, and the last square contains one whole pentomino.
In the following 3 (resp.6) solutions, the whole pentomino in the last square is the F.
Here, the I and T are cut.


In the following solutions, the whole pentomino in the last square is the T.
Here, the I and F are cut. Since the first three squares are always built in the same manner, only the last square is drawn for the solutions
The last two solutions have a speciality: The diagonal cut may not only be made under 45°, but under various angles. (The additional drawing of the grey triangles shall indicate some of the possible cuts.)
First case: 0° < φ ≤ 45°.
Second case: 45° ≤ φ ≤ arctan(2) = 63,43494882°.
So there is an infinity of solutions."


 Aad van de Wetering found an solution:



Helmut generalized the solution by varying the angle of the cuts.

Do you know other solutions?