Pentomino's in 4 vierkanten
Alexandre Muñiz

Op facebook van Puzzle Fun vonden we dit puzzeltje.
Neem een pentominoset

Knip diagonaal twee pentomino's
Je mag elke pentomino maar éénmaal knippen.
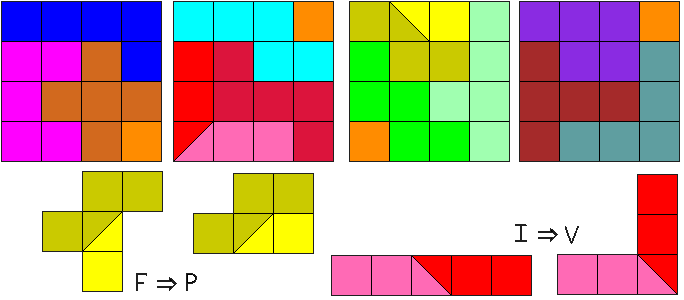
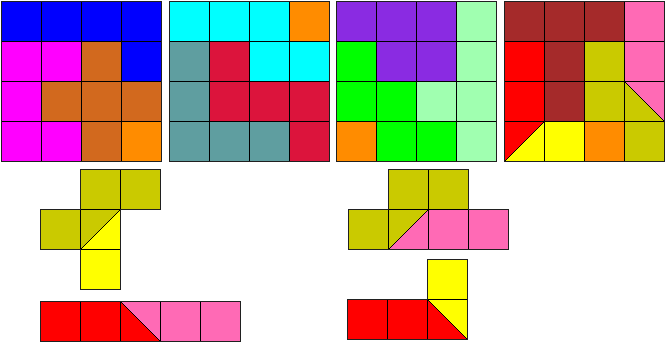
Leg de bekomen 14 stukken samen met 4 monomino's in vier 4x4 vierkanten.
We hadden diagonaal knippen waarschijnlijk slecht begrepen en vonden de volgende oplossing

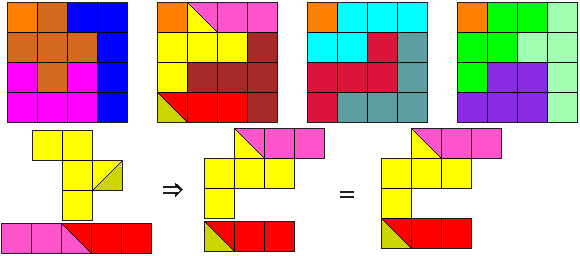
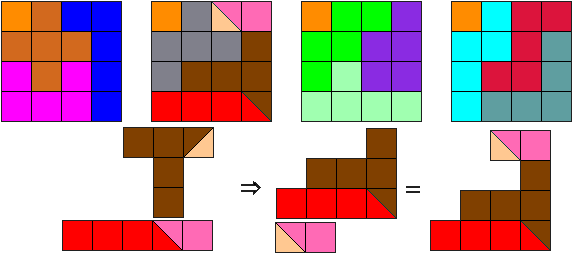
Toch vinden we diagonaal versnijden over twee vierkanten ook mooi.
Met deze versnijding zijn er heel veel mogelijkheden om de vierkanten te vullen.
Vind je nog andere versnijdingen van dit soort?
Van Helmut Postl hadden we reeds veel eerder een document gekregen met oplossingen maar we waren het uit het oog verloren.
"Some solutions have a speciality: The diagonal cut may not only be made under 45°, but under various angles. (The additional drawing of the grey triangles shall indicate some of the possible cuts.)
First case: 0° < φ ≤ 45°.
Second case: 45° ≤ φ ≤ arctan(2) = 63,43494882°.
So there is an infinity of solutions."

 



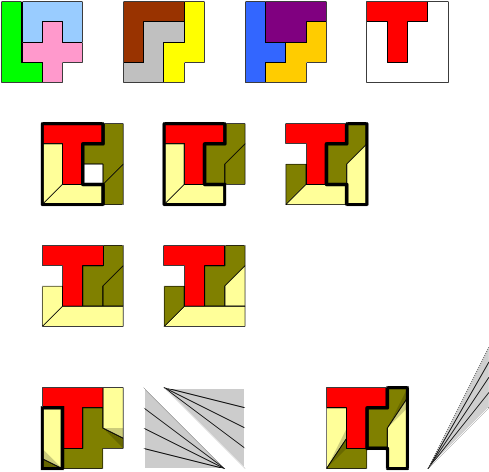
We begonnen met uit te zoeken welke pentomino's diagonaal versneden kunnen worden tot een andere pentomino
http://www.pentomino.classy.be/p60versnijden.html
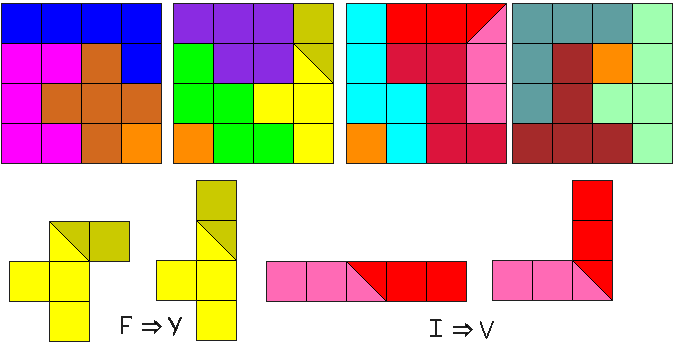
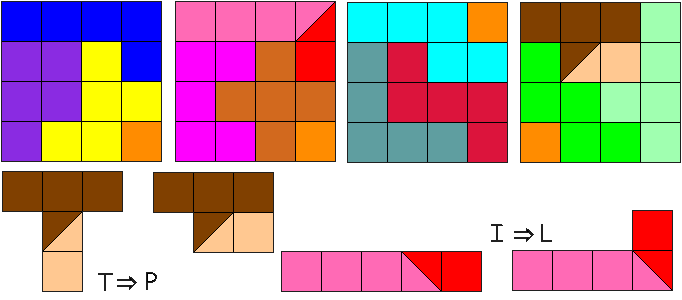
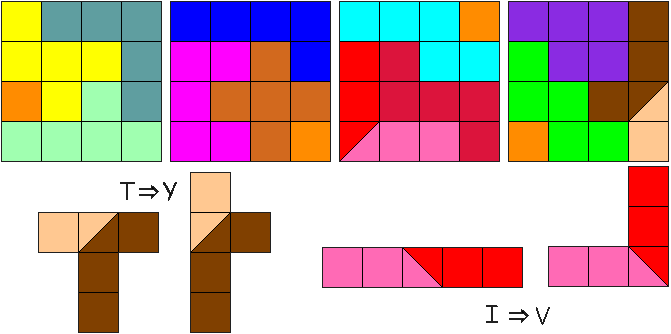
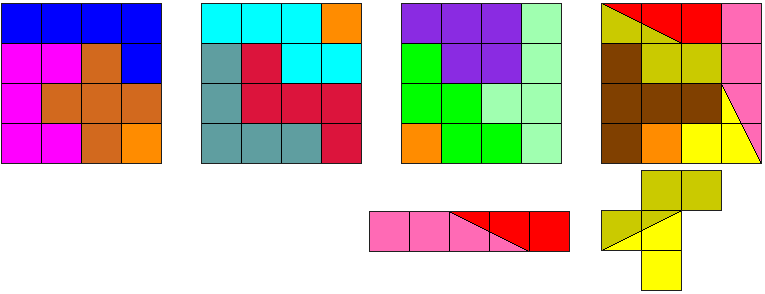
We zochten oplossingen met een knip langs de diagonaal van één vierkantje.
We vonden een aantal oplossingen waarbij de I-pentomino verknipt werd tot L of V-pentomino. De I-pentomino moet zeker verknipt worden want die past niet binnen een vierkant van 4x4.
Helmut: "There seems to be no way to cut the I-pentomino twice, so the second cut has to be made on a different pentomino"
In de opgave stond dat er twee pentomino's moeten versneden worden maar men kan inderdaad geen vier vierkanten vullen met 4 monomino's en een pentominoset zonder de I-pentomino en een tweede exemplaar van gelijk welke andere pentomino.

Je kan natuurlijk altijd de volledige pentomino vervangen door de 2 stukken die dezelfde pentomino vormen en andersom en dan krijg je een andere oplossing.
Soms vormen 2 of meer stukken een symmetrische vorm binnen een vierkant en dan kan je spiegelen en bekom je eigenlijk een andere oplossing.
Helmut syuurde ons een mooi gestructureerd document dat je kan zien op de Engelse versie
http://www.pentomino.classy.be/p60e.html

We vonden ook een oplossing waarbij F en I-pentomino een L-tetromino en een hexomino worden

We probeerden ook met 2 pentomino's tot de I-tromino en een heptomino maar vonden geen oplossingen.
Aad van de Wetering vond er wel één :"Leuk idee weer! De F en de I zitten versneden in het tweede vierkant tot tro- en heptomino.
Eventueel zelfs één dekamino."

En Aad vond er eentje met een domino en  een octomino, tevens een dekamino