Jan Guichelaar
Het idee komt uit het tijdschrift Pythagoras
NOOTJE KRAKEN 56: LIJN TREKKEN
Neem een stukje ruitjespapier en een pen. Teken langs de lijntjes een gesloten lijn met een lengte van 10. Je mag een al getekend punt niet nog een keer aandoen (behalve het begin/eindpunt). Twee figuren die door spiegelen of draaien in elkaar overgaan tellen maar voor één.
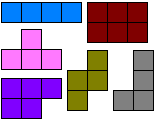
Let erop dat gelijke omtrek niet noodzakelijk dezelfde oppervlakte betekent.
Met deze polyomino's kan je een rechthoek leggen. De totale oppervlakte is 27 dus dus een rechthoek van 3x9. Er zijn 19 oplossingen.
Met deze stukjes kan men ook figuren maken met symmetrie-assen of met een symmetriemiddelpunt.
Hieronder een paar voorbeelden.
Duw op de opgave en je ziet de oplossingen.
|
|
|
|
|
|
|
|
|
|
Van George Sicherman (USA) kregen we de 10 volgend oplossingen.
|
|
|
|
|
|
|
|
|
|
Andere oplossingen gevonden?
Je kan deze opgave natuurlijk uitbreiden en bijvoorbeeld alle polyomino's zoeken met een omtrek van 12.
