Vierlandenpunt
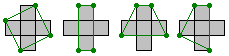
 We kregen een mail van Victor Stok: "Weer eens wat bedacht. Wie weet wat je ermee kan.
Nog zelf geen oplossingen gezocht."
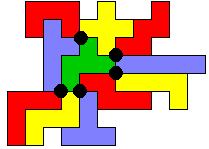
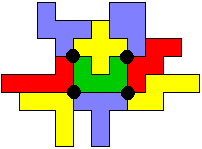
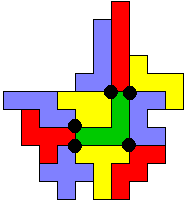
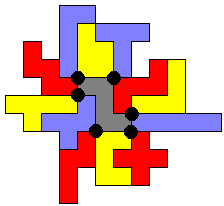
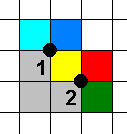
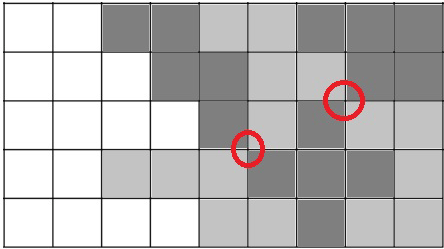
In onderstaande figuur zie je dat er 2 punten omcirkeld zijn. Op deze plaatsen raken 4 pentomino's elkaar met de hoekpunten. Dit noemt Victor een vierlandenpunt. De pentominorechthoek is niet af. Kun je een rechthoek maken met zoveel mogelijke vierlandenpunten?

Leuk weetje:
van 1839 tot 1920 was er een vierlandenpunt met België, Nederland, Pruisen (later Duitsland) en Neutraal Moresnet. Het laatste 'land' had geen staatshoofd en regering en is in 1920 opgegaan in België.
Opmerking: de rechthoek van Victor kan niet afgewerkt worden!

We kregen al meteen oplossingen binnen van Aad van de Wetering
"In een 9x5 maximaal 3 vierlandenpunten: 9 oplossingen"

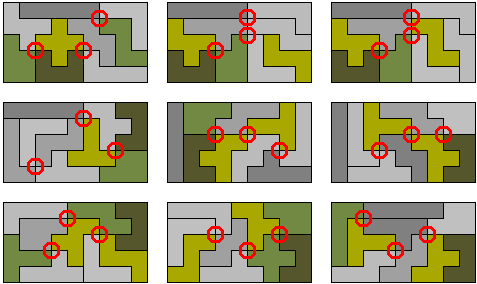
We vonden het echter mooier van vierlandenpunten te zoeken met een set pentomino's.
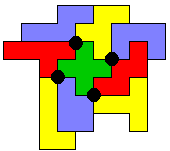
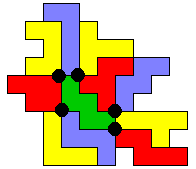
Ook hiervoor stuurde Aad (van de Wetering) opnieuw 9 oplossingen met 4 vierlandenpunten.


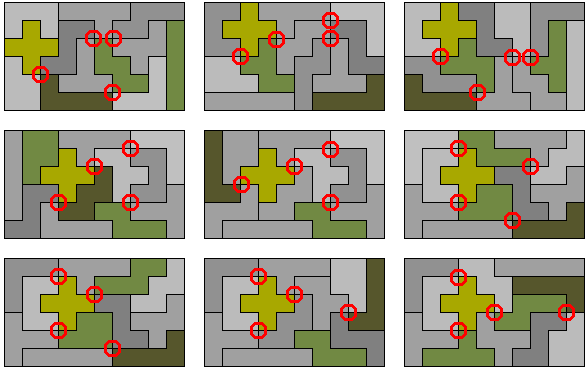
George Sicherman stuurde ons ook deze 9 oplossingen toe.


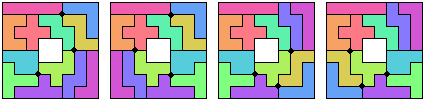
George stuurde ook 4 oplossingen met 3 vierlandenpunten in een 8x8 vierkant met een gat in het midden van 2x2.


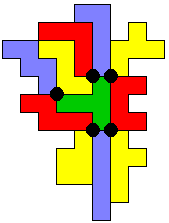
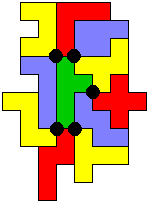
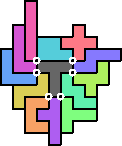
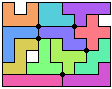
En George stuurde nog een 7x9 (met een gat) met 5 vierlandenpunten.

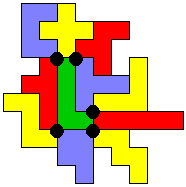
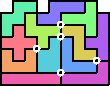
Hij wou het nog beter doen en stuurde er eentje van 7x9 zonder gat


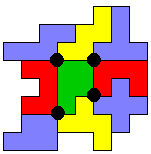
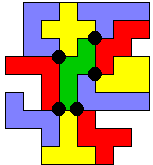
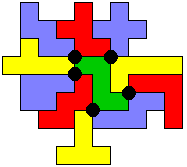
Aad zocht verder naar een maximale oplossing en stuurde 2 oplossingen in 8x8 met 5 vierlandenpunten.
Schitterend!

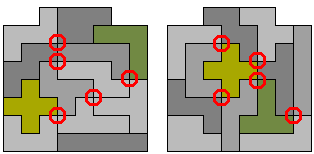
Aad merkte op dat in de laatste figuur de X 4 vierlandenpunten heeft.
Zou 4 het maximaal aantal vierlandenpunten zijn dat een pentomino kan hebben? Zie verder.
Hij mailde bovendien dat in de eerste figuur de punten op een gelijkbenige driehoek liggen met zijden 4, 2V5 en 2V5.
De figuur gevormd door de 5 vierlandenpunten heeft een symmetrieas.
Wat goed gezien!

Victor stuurde nog een paar vragen:
Is het ook mogelijk om een figuur te maken waarbij het vierlandenpunt (of meerdere vierlandenpunten) op de symmetrieas ligt (liggen) ?
Kan je een figuur maken waarbij het vierlandenpunt het symmetriemiddelpunt is?
Aad stuurde meteen een rechthoek die meteen antwoord is op beide vragen.
Wat is hij slim! Of moeten we Poly3D leren gebruiken?


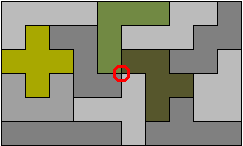
Maar Victor heeft steeds nieuwe variaties:
Kun je bij 1 pentomino in een figuur meer vierlandenpunten hebben? Wat is het maximum?
George Sicherman mailde terecht: "Of course five crosspoints is the maximum for a single pentomino.
With six, the pentomino would have six "strong" neighbors and six "weak" neighbors. That is 12 neighbors--too many!"

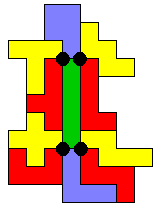
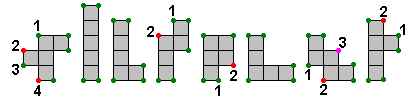
We zochten het uit voor de F. We vonden er 5. Hiervoor gebruikten we een set pentomino's.


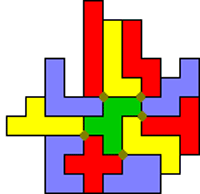
Aad van de Wetering deed het echter met minder.Dit was iets moeilijker dan met een set.

We zochten het uit voor de andere pentomino's. Voor P, U en X vonden we maar 4 vierlandenpunten

Bij de  I-pento en bij de U-pento zijn de vierlandenpunten de hoekpunten van een rechthoek en bij de X-pento vormen de vierlandenpunten een vierkant.(Er is dus heel wat symmetrie te vinden.)
Bij de I-pentomino hebben we 10 pentomino's nodig, bij de rest hebben we de vier landenpunten kunnen vormen met nog 8 andere pentomino's

Voor F, L, N, T, V, W, Y en Z vonden we 5 vierlandenpunten waarbij we naast de gegeven pentomino er nog 10 nodig hadden.

Merk op: de vijfhoek gevormd door de 5 vierlandenpunten bij de V-pentomino heeft een symmetrie-as.

De laatste oefening gaf aanleiding tot een nieuwe opgave.
Maak met een pentominoset 6 vierlandenpunten rond een andere pentomino.

Onmiddellijk stuurde George Sicherman een andere oplossing namelijk met de T-pentomino

De zeshoek gevormd door de 6 vierlandenpunten heeft een symmetrieas.

We zijn er van overtuigd dat T en Z de enige 2 pentomino's zijn die 6 vierlandenpunten hebben.
We proberen het uit te leggen met de volgende tekeningen.
De grijze vierkanten behoren tot een pentomino.

De punten 1 en 2 kunnen nooit beide vierlandenpunten zijn want het gele vierkantje zit ingesloten en kan dus nooit tot een pentomino behoren.

De punten 1 en 2 kunnen niet gelijktijdig een vierlandenpunt zijn en dat geldt ook voor de punten 3 en 4 van F-pentomino.
Het punt 3 van de W-pento kan om dezelfde reden nooit het vijfde vierlandenpunt zijn

.
Bij U-pento kunnen maar 4 vierlandenpunten zijn.
In de andere punten kunnen nooit 4 pento's samen komen.
(geel vierkant zit ingesloten)


Bij de X-pento zijn 4 vierlandenpunten ook het maximaal aantal. Soms vormen de vierlandenpunten een vierkant met zijde V5 , een rechthoek of een gelijkbenig trapezium.