Eén voor
alles, alles voor één
Het idee kregen we van Victor Stok
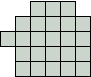
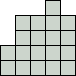
Dit is de kleinste vorm waarin je alle pentomino's kan leggen.
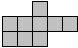
Hij bestaat uit 9 vierkantjes.
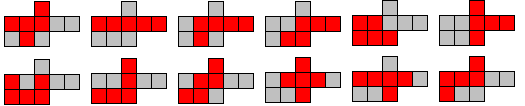
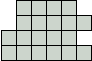
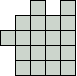
Wat is de kleinste vorm waarin elke combinatie van 2
verschillende pentomino's past?
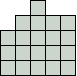
Victor Stok begon met een vorm met 15 vierkantjes.
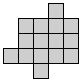
We kregen er eentje van Aad van de Wetering met 14.
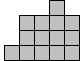
Kan je beter? We denken het niet.
Kan je echter nog een andere vorm?
Stuur jou oplossing.
Wat is de kleinste vorm waarin elke
combinatie van 3 verschillende pentomino's past?
Aad van de Wetering stuurde 3 verschillende vormen van
20 vakjes waarin alle 220 combinaties van 3 verschillende pentomino's
passen.
Wil je voor de eerste vorm alle oplossingen zien druk dan op de vorm.
 |
 |
 |
|
|
|
|
|
En wat is de kleinste vorm waarin elke
combinatie van 4 verschillende pentomino's past?
We kregen het volgende antwoord van George Sicherman "I have found
some 24-ominoes that contain all sets of four distinct pentominoes. One of
them even has a hole!"
We controleerden of alle 495 combinaties erin kunnen.
Wil je alle oplossingen zien? Druk dan op de bovenstaande
vorm.
Aad van de Wetering stuurde ook een vorm waarin alle
495 combinaties in kunnen. We geloven hem!
|
|
