Aad van de Wetering merkte op dat er 16 zijn! Dank
Hieronder staan nog eens de pentomino's met hun overeenkomende letters.

Verdeel de gele vakjes van het paasei in pentomino's zodat geen twee pentomino's met
dezelfde vorm (ook niet gedraaid of gespiegeld) een zijde gemeen hebben. Een
vierkantje met een letter in moet deel uit maken van de pentomino met
dezelfde naam (zie hierboven).
De totale oplossing moet twee symmetrieassen hebben.
|
Oplossers:
Odette De Meulemeester - BelgiŽ
Aad van de Wetering - Nederland
Aad Thoen - Nederland
Patrick Oufflin - BelgiŽ
George Sicherman - USA
Nicole Verschuere - BelgiŽ |
Oplossers:
Odette De Meulemeester - BelgiŽ
Aad van de Wetering - Nederland
Aad Thoen - Nederland
Patrick Oufflin - BelgiŽ
George Sicherman - USA
Nicole Verschuere - BelgiŽ |
Oplossers:
Odette De Meulemeester - BelgiŽ
Aad van de Wetering - Nederland
Aad Thoen - Nederland
George Sicherman - USA
Nicole Verschuere - BelgiŽ
Luna De Croo - BelgiŽ |
|
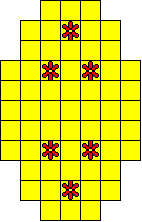
Oplossers:
Odette De Meulemeester - BelgiŽ
Aad van de Wetering - Nederland
Aad Thoen - Nederland
George Sicherman - USA
Nicole Verschuere - BelgiŽ
Luna De Croo - BelgiŽ |
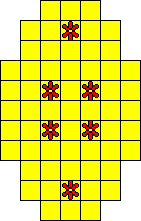
Oplossers:
Odette De Meulemeester - BelgiŽ
Aad van de Wetering - Nederland
Aad Thoen - Nederland
George Sicherman - USA
Nicole Verschuere - BelgiŽ |
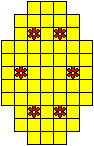
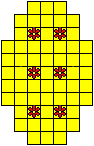
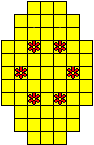
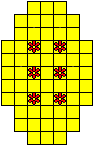
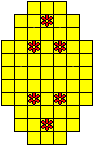
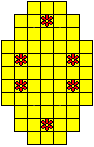
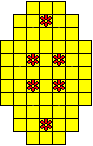
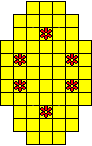
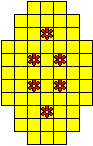
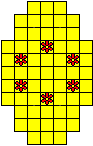
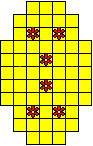
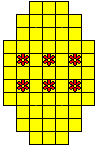
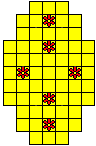
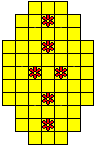
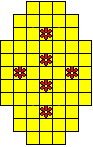
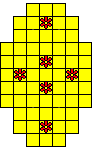
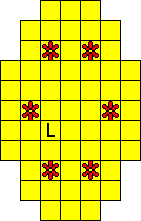
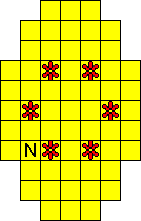
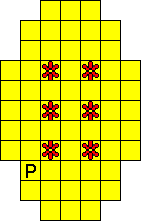
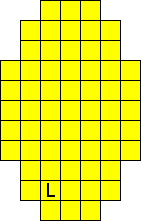
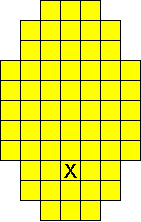
Plaats pentomino's op de gele vakjes van het paasei zodat geen twee pentomino's met
dezelfde vorm (ook niet gedraaid of gespiegeld) een zijde gemeen hebben. Een
vierkantje met een letter in moet deel uit maken van de pentomino met
dezelfde naam (zie hierboven). Daarnaast moet je zes bloemetjes plaatsen die
noch de rand noch elkaar mogen raken (ook geen puntcontact)
De totale oplossing moet twee symmetrieassen hebben.
Er is telkens juist ťťn oplossing.
|
Oplossers:
Odette De Meulemeester - BelgiŽ
Aad van de Wetering - Nederland
Nicole Verschuere - BelgiŽ |
Oplossers:
Odette De Meulemeester - BelgiŽ
Aad van de Wetering - Nederland
Nicole Verschuere - BelgiŽ |
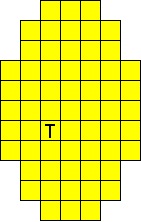
Oplossers:
Odette De Meulemeester - BelgiŽ
Aad van de Wetering - Nederland
Nicole Verschuere - BelgiŽ |
We hebben ook een paasei gemaakt met maar ťťn bloemetje.
De totale oplossing heeft twee symmetrieassen.
Bedenk dat een vierkantje van F, L, N, P, V, W, Y en Z nooit op een symmetrieas
kan liggen.
|
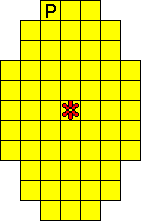
Oplossers:
Odette De Meulemeester - BelgiŽ
Aad van de Wetering - Nederland
Aad Thoen - Nederland
Nicole Verschuere - BelgiŽ |
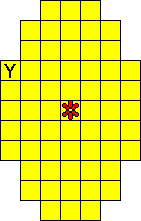
Oplossers:
Odette De Meulemeester - BelgiŽ
Aad van de Wetering - Nederland
Aad Thoen - Nederland
Nicole Verschuere - BelgiŽ |
|
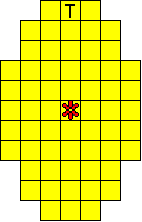
Oplossers:
Odette De Meulemeester - BelgiŽ
Aad van de Wetering - Nederland
Aad Thoen - Nederland
Nicole Verschuere - BelgiŽ |
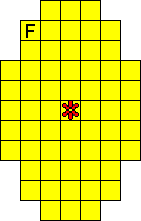
Oplossers:
Odette De Meulemeester - BelgiŽ
Aad van de Wetering - Nederland
Aad Thoen - Nederland
Nicole Verschuere - BelgiŽ |
|
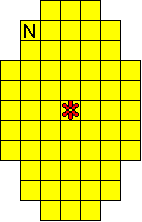
Oplossers:
Odette De Meulemeester - BelgiŽ
Aad van de Wetering - Nederland
Aad Thoen - Nederland
Nicole Verschuere - BelgiŽ |
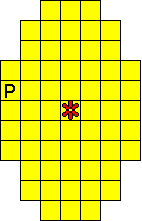
Oplossers:
Odette De Meulemeester - BelgiŽ
Aad van de Wetering - Nederland
Aad Thoen - Nederland
Nicole Verschuere - BelgiŽ |
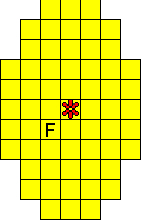
Oplossers:
Odette De Meulemeester - BelgiŽ
Aad van de Wetering - Nederland
Aad Thoen - Nederland
Nicole Verschuere - BelgiŽ |