Het raster (10x10) is reeds verdeeld in decomino's.
Elke decomino moet je verdelen in twee pentomino's zodat in het raster geen
twee pentomino's met dezelfde vorm (ook niet gedraaid of gespiegeld) een
zijde gemeen hebben.
|

Oplossers
George Sicherman - USA
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Bob Henderson - USA
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Nicole Verschuere - BelgiŽ |
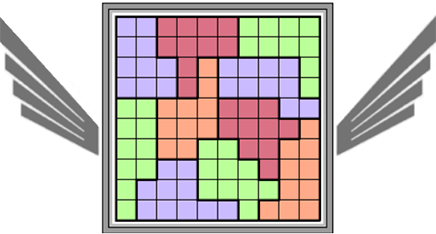
Oplossers
George Sicherman - USA
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Nico Looije - Nederland
Jenard Cabilao - Filipijnen |
|
Elke decomino is op 3 verschillende manieren te verdelen in 2
pentomino's.

Oplossers
George Sicherman - USA
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Nico Looije - Nederland
Aad van de Wetering - Nederland
|
Elke decomino is op 3 verschillende manieren te verdelen in 2
pentomino's.

Oplossers
George Sicherman - USA
"Aad Thoen likes Art Deco"
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
|
|
Elke decomino is op 3 verschillende manieren te verdelen in 2
pentomino's.

Oplossers
George Sicherman - USA
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Nico Looije - Nederland
|
Hier is een decomino die op 4 verschillende manieren te verdelen in 2
pentomino's.
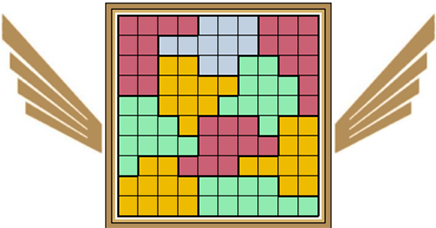
Oplossers
George Sicherman - USA
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Nico Looije - Nederland |
|
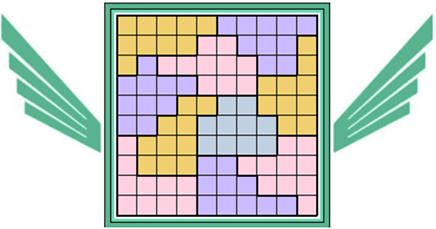
Oplossers
George Sicherman - USA
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Nico Looije - Nederland
|
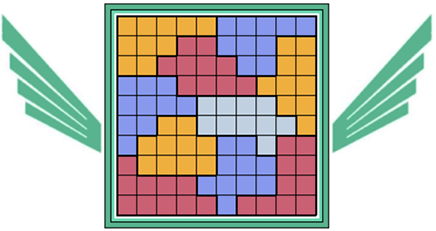
Oplossers
George Sicherman - USA
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Nico Looije - Nederland
Aad van de Wetering - Nederland |
|
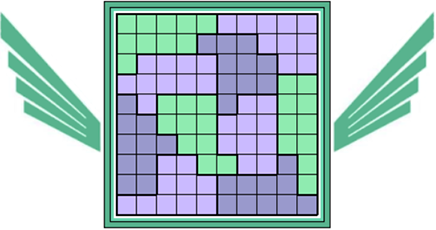
Oplossers
George Sicherman - USA
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Nico Looije - Nederland |
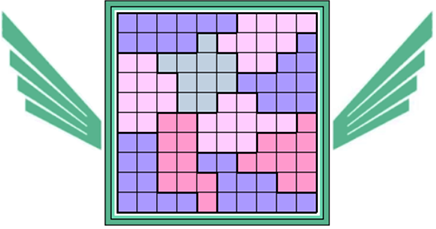
Oplossers
George Sicherman - USA
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Nico Looije - Nederland
Aad van de Wetering - Nederland
"A kind of a milestone: the decoth decorous!
5 possible PY in this puzzle, 3 realized." |
|
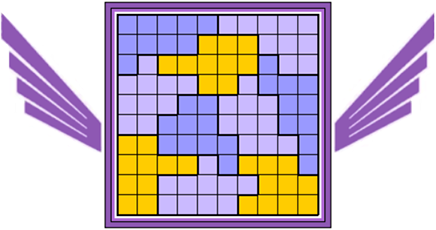
Oplossers
George Sicherman - USA
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Nico Looije - Nederland
Aad van de Wetering - Nederland
Bob Henderson - USA
Jenard Cabilao - Filipijnen |
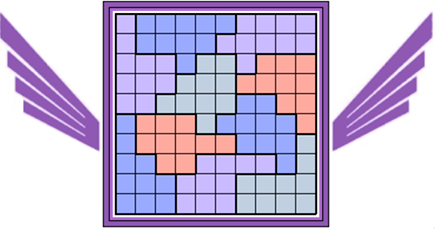
Oplossers
George Sicherman - USA
Odette De Meulemeester - BelgiŽ
Aad van de Wetering - Nederland
Aad Thoen - Nederland
"Again a majority of PY"
Nico Looije - Nederland |
|
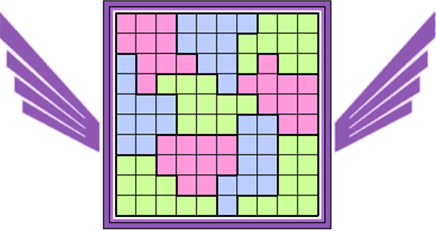
Oplossers
George Sicherman - USA
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Nico Looije - Nederland |

Oplossers
George Sicherman - USA
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Nico Looije - Nederland |
|

Oplossers
George Sicherman - USA
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Nico Looije - Nederland |
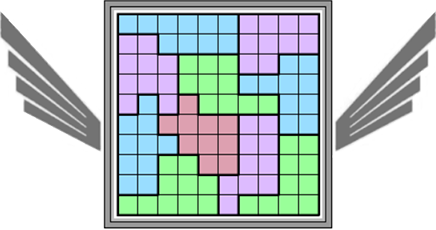
Oplossers
George Sicherman - USA
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Nico Looije - Nederland |
Bob :"I write special-purpose programs to make and solve puzzles. They are
mostly sequential-movement puzzles, but when I started 35 years ago, I wrote
a computer program to fill a chess board with the 12 pentominoes. Most of my
solutions for your pentomino puzzle competitions were found using programs
that I wrote. . . now it is easier to use
Aad's
powerful "FlatPoly" program!
I will try to make some new decomino puzzles for you."
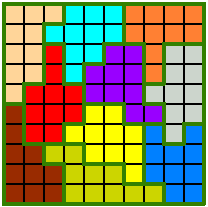
Onderstaande decomino kregen we van George dubbel. Kan je hem terug
vinden?
OdetteDM@outlook.com

![]()
















