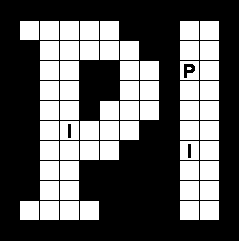
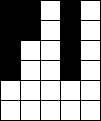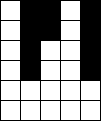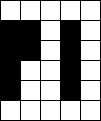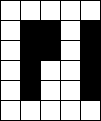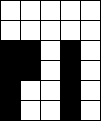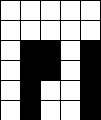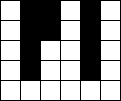Heel veel dank aan Aad van de Wetering voor het maken van de puzzels.
Omdat iedereen de Pi-dag (14 maart) moet vieren zijn onze pentominous voor iedereen van heel makkelijke tot heel moeilijke.
Wie verdient een PI-beker?
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Nicole Verschuere - BelgiŽ
Edo Timmermans - Nederland
Thijs Notenboom - Nederland
Hein van Winkel - Nederland
Ton Tillemans - Zwitserland
Margo en Arthuur De Croo - BelgiŽ
Floor De Croo - BelgiŽ
Ton Tillemans - Zwitserland
Jan Kok - Nederland
Matthijs Coster - Nederland
"Leuke en lekkere puzzel"
Puzzel
Eregalerij
|
|
|
|
|
|
Hieronder staan nog eens de pentomino's met hun overeenkomende letters.

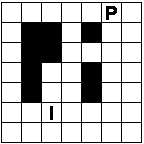
In raster van 5x6

Verdeel de witte vakjes in pentomino's zodat geen twee pentomino's met
dezelfde vorm (ook niet gedraaid of gespiegeld) een zijde gemeen hebben.
Bij sommige opgaven krijg je een extra voorwaarde i.p.v. een hint omdat er
juist ťťn oplossing zou zijn.
Oplossers: |
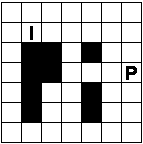
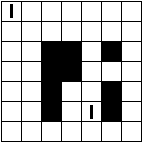
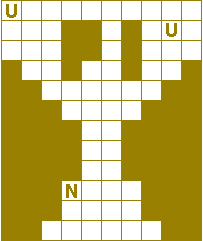
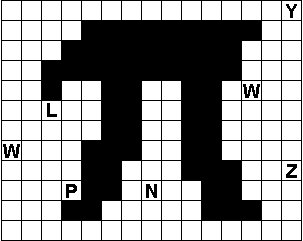
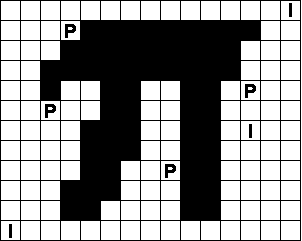
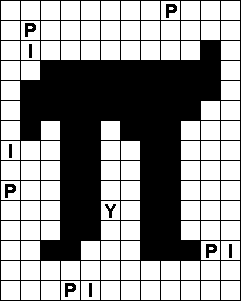
Verdeel de witte vakjes in pentomino's zodat geen twee pentomino's met
dezelfde vorm (ook niet gedraaid of gespiegeld) een zijde gemeen hebben. Een
vierkantje met een letter in moet deel uit maken van de pentomino met
dezelfde naam (zie hierboven).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
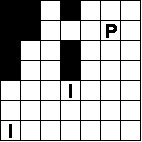
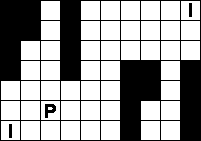
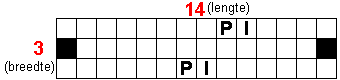
In de volgende pentominoes is 'PI' gevuld met juist een
set pentomino's.
Benaderingen van PI
Op 0,01 nauwkeurig en te klein Op 0,0001 nauwkeurig en te klein Bij de twee volgende pentominoes zijn sommige zijden van de pentomino's reeds getekend. (zie
rode lijntjes waarmee we 3.14 vormen)
Een grapje van Aad. Schitterend gevonden!
Een uitgebreide verzameling pi-rebussen staan op
https://glorieuxronse.classy.be/droedels.html Chichťn ItzŠ
PIpet Voornaam? Als toemaatjes
een brede PI Een mooie vondst: Oplossingen of tekeningen die we mogen plaatsen
Ode aan
Flat Poly
Voor onze PI-dag van 2024 kregen we van George Sicherman de volgende leuke
PI-pentoe:
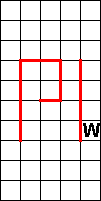
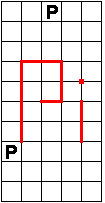
Bij de twee volgende pentominoes zijn sommige zijden van de pentomino's reeds getekend. (zie
rode lijntjes waarmee we PI vormen)
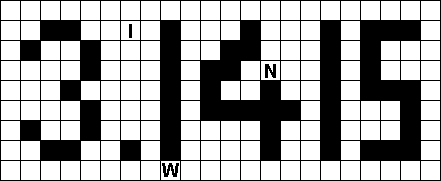
Het punt op de i betekent een kruispunt van twee wegen, dus de vier vakjes
behoren bij vier niet dezelfde pentominoís
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Thijs Notenboom - Nederland
Hein van Winkel - Nederland
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Thijs Notenboom - Nederland
Hein van Winkel - Nederland
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ

Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Hein van Winkel - Nederland
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ

Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Hein van Winkel - Nederland
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ

Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Hein van Winkel - Nederland
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Hein van Winkel - Nederland
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Hein van Winkel - Nederland
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Hein van Winkel - Nederland
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ
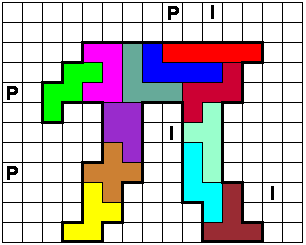
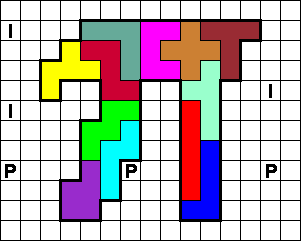
Als je de witte vakjes in pentomino's verdeelt mogen deze ook geen zijde
gemeen hebben met een zelfde pentomino (ook niet gedraaid of gespiegeld)
waarmee de 'PI' gevuld is.
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Jenard Cabilao - Filipijnen
Aad Thoen - Nederland
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Jenard Cabilao - Filipijnen
Aad Thoen - Nederland
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ
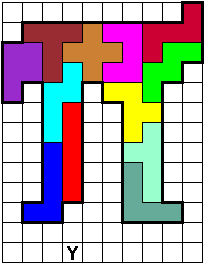
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Jenard Cabilao - Filipijnen
Aad Thoen - Nederland
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
Merel Lefebvre - BelgiŽ
Nicole Verschuere - BelgiŽ
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ
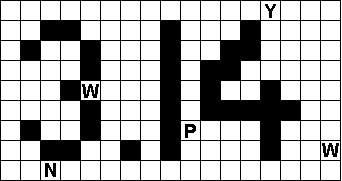
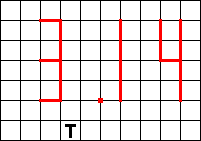
Het punt na de 3 (komma) betekent een kruispunt van twee wegen, dus de vier vakjes
behoren bij vier niet dezelfde pentominoís
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
"Moeilijk"
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Nico Looije - Nederland
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ
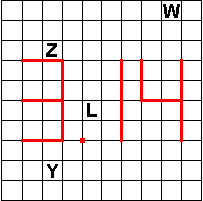
In de twee volgende pentominoes is het aantal verschillende buurvakjes soms gegeven.
Een buur is zowel orthogonaal als diagonaal.
Meer uitleg over
buren

Samen met buren
gaan we de pi-dag vieren
Heel veel dank aan Aad
De rasters zijn 3.14

Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Aad Thoen - BelgiŽ
Nico Looije - Nederland
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ

Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Nico Looije - Nederland
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
Het mooist vinden we als leerlingen zelf 3D-pi -rebussen maken. Voorbeelden
kan je zien op
https://pentomino.classy.be/schoolrebussen.html
Van vier rebussen maakte Aad pentominoes.
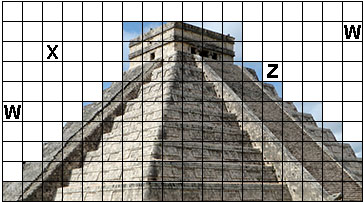
Mexico

Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ

Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ

Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
Patrick Oufflin - BelgiŽ
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
Marcel Peyskens - BelgiŽ
Lente Vansonhoven - BelgiŽ
Leen Vanarwegen - BelgiŽ
George Sicherman - USA
Nicole Verschuere - BelgiŽ
Invuldocument

Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Patrick Oufflin - BelgiŽ
Lente en Jade Vansonhoven - BelgiŽ (+/- 20 min)
Eddy Moreau - BelgiŽ (6 min)
Marieke De Croo - BelgiŽ (5 min)
Nico Looije - Nederland
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ
Invuldocument
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
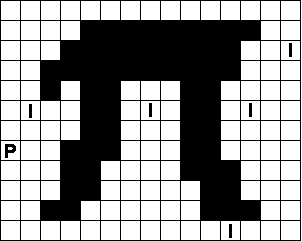
Zonder hints, maar je mag maar vier verschillende pentominoís
gebruiken!

Wil je tip ga dan met de muisaanwijzer over de opgave.
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Nico Looije - Nederland
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ
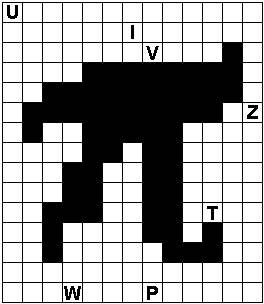
De eerste andere PI kregen we van Edo Timmermans.
Aad maakte er drie pentominoes mee. Alhoewel?
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Edo Timmermans - Nederland
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ

Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Edo Timmermans - Nederland
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ
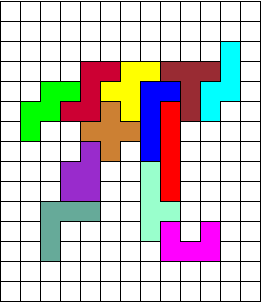
De gekregen PI van Edo is juist op ťťn manier te vullen met een
pentominoset.
Aad kon er echter geen pentominoe mee maken. Kan je vinden waarom niet?
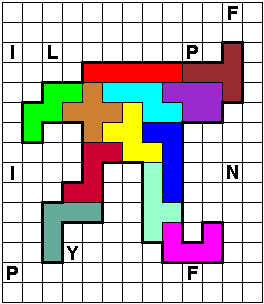
We veranderden PI een beetje. Toen ging het wel.
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Edo Timmermans - Nederland
Nico Looije - Nederland
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ

Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Jenard Cabilao - Filipijnen
Nico Looije - Nederland
Aad Thoen - Nederland
Edo Timmermans - Nederland
"In ieder geval: een symmetrische puzzel met symmetrische hints
die een unieke oplossing heeft moet een symmetrische oplossing
hebben."
Patrick Oufflin - BelgiŽ
Luc Gheysens - BelgiŽ
Nicole Verschuere - BelgiŽ
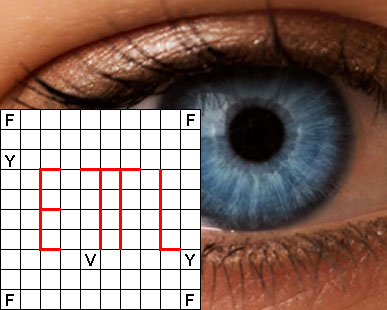
"Met PI in zee"
Matthijs Coster - Nederland
"Als de puzzel niet een symmetrische oplossing heeft dan heb je een tweede oplossing door 180 graden te roteren."
Thijs Notenboom - Nederland
Jan Kok - Nederland
"12-3-21 is datum die past bij een symmetrische oplossing"
Eddy Moreau - BelgiŽ
Ton Tillemans - Zwitserland
Marcel Peyskens - BelgiŽ
Ilse De Boeck - BelgiŽ
Leen Vanarwegen - BelgiŽ
George Sicherman - USA
Willy Bijnens - BelgiŽ
Gioia Everaerts - BelgiŽ
Kate Jones - USA
Lieven Van Rijckeghem - BelgiŽ
Els Coussement - BelgiŽ
Oplossers:
Nico Looije - Nederland
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Jenard Cabilao - Filipijnen
Ton Tillemans - Zwitserland
Nicole Verschuere - BelgiŽ
Ilse De Boeck - BelgiŽ
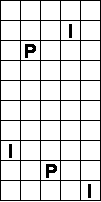
Oplossers:
George Sicherman - USA
"Now you know that sometimes Pi can be rectangular."
Aad van de Wetering - Nederland
Odette De Meulemeester - BelgiŽ
Aad Thoen - Nederland
Matthijs Coster - Nederland
Els Coussement - BelgiŽ
Helmut Postl - Oostenrijk
"Wow, George has accomplished the impossible: squaring the circle! :-)
Beautiful rectangle!"
Nicole Verschuere
- BelgiŽ
Edo Timmermans - Nederland
Ilse De Boeck - BelgiŽ
Jenard Cabilao - Filipijnen
Wil je nog meer

Om de Pi-dag te vieren vind je Pi-sudoku's en pi-tectonics op
pentomino.classy.be/pipuzzel.html
![]()