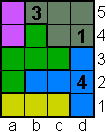
in de T-pentomino(blauw gebied) moet 1 op b2, c2 of d1 staan => 1 kan niet op c1 => 1 staat op a1 of b1 => 1 kan niet op a2 maar 1 kan ook niet op c3 => 1 staat op a3, b3 of b4 => 1 kan niet op a4 => 1 op a5 en 2 op a4
Oplossing van Pi-tectonic 4
|
|
op a1,b1 en c1 staan 1,2 en 3 => op b2 kan alleen 5 staan => in
F-pentomino (groen gebied) kan 5 alleen op b4 => in P-pentomino
(grijs gebied) kan 5 alleen op d5 in de T-pentomino(blauw gebied) moet 1 op b2, c2 of d1 staan => 1 kan niet op c1 => 1 staat op a1 of b1 => 1 kan niet op a2 maar 1 kan ook niet op c3 => 1 staat op a3, b3 of b4 => 1 kan niet op a4 => 1 op a5 en 2 op a4
|
|
|
x, y en z zijn 1, 2 en 3 |
|
|
in de T-pentomino moet z op d3 en dan y op d1 en dus x op c2 x kan in de F-pentomino alleen op a3 de buren van c3 zijn 1, 4, x en z dus staat y op c3 y en z kunnen geen 1 zijn want op d4 staat 1=> x=1
|
|
|
y en z zijn 2 en 3 dus de buren van c4 zijn 1, 2, 3 en 5 => 4 staat op c4 => 2 op c5 |
|
|
4 moet op a2 =>z op b3 |
|
|
=> z kan geen 2 zijn => z=3 en y = 2 |
|
Opmerking: 3 op b5 in de gegevens is totaal overbodig en dient alleen
omdat de gegeven cijfers 3, 1 en 4 zouden zijn (pi).
Dit is zeker niet de enige oplossingsmethode.