2-2 Symmetrie in figuren bestaande uit 3 pentomino's

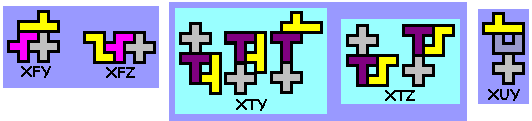
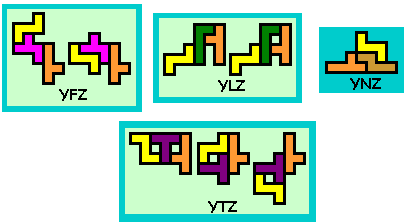
Dank zij Aad van de Wetering zijn programma denken we dat we alle figuren gevonden hebben bestaande uit 3 pentomino's waarbij de middelste met beide buren telkens een figuur vormt (bestaande uit 2 pentomino's) die een symmetrie-as heeft.
Er zijn er 412

























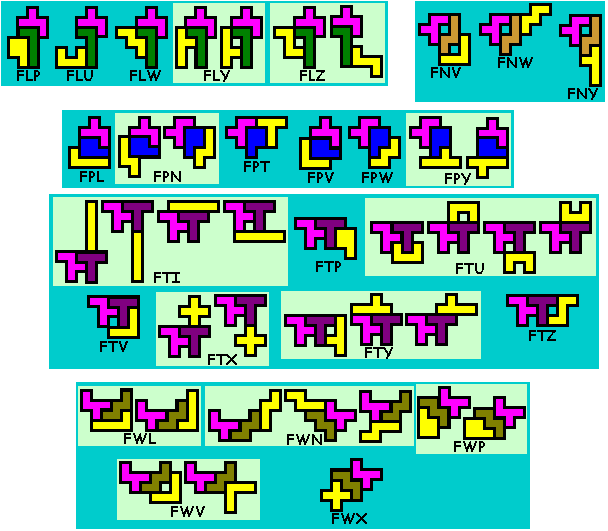
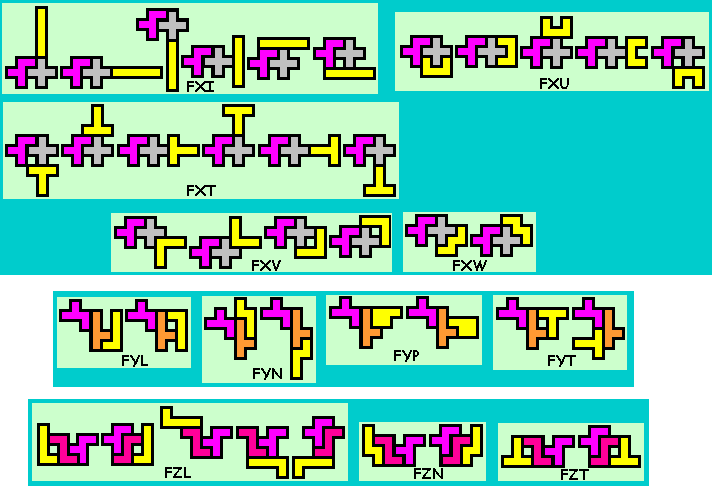
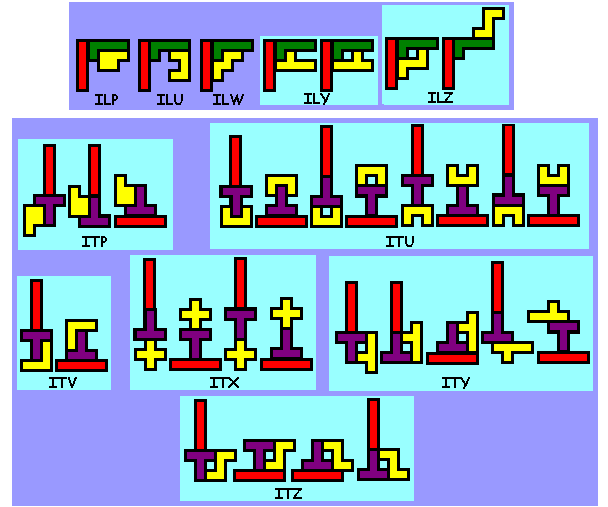
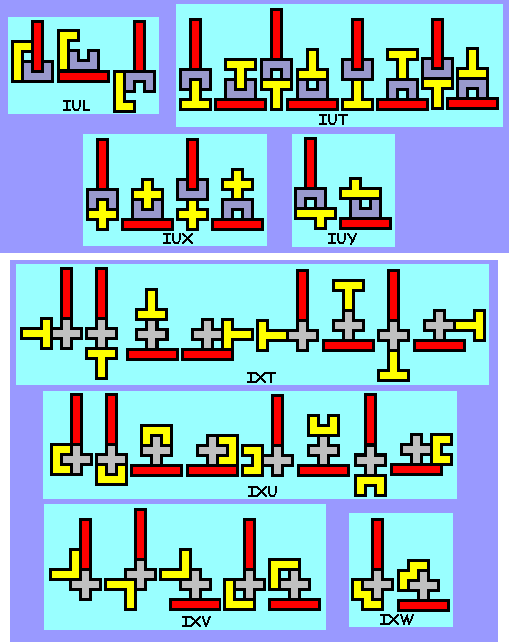
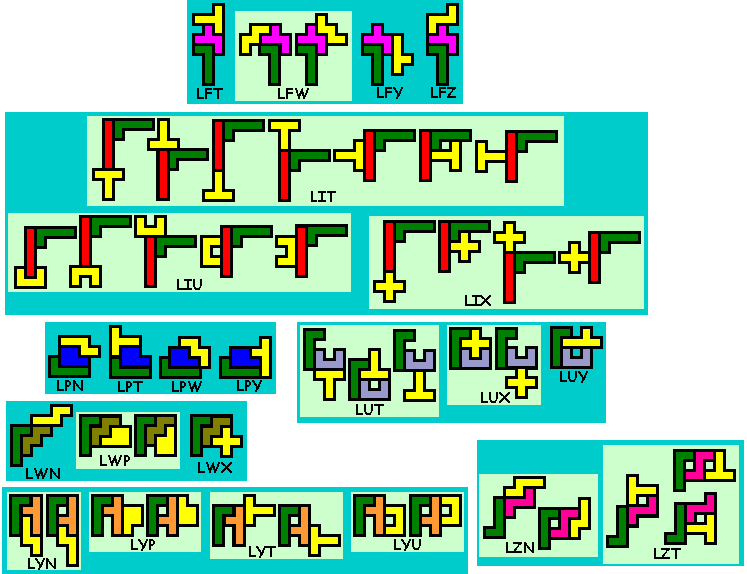
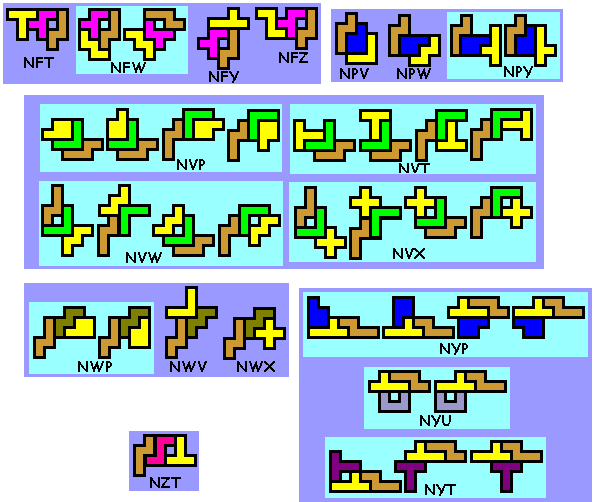
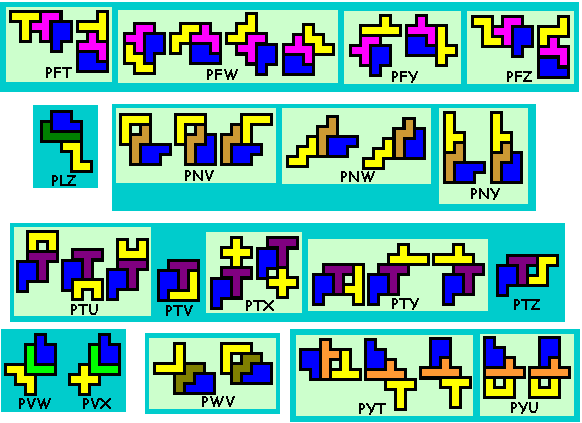
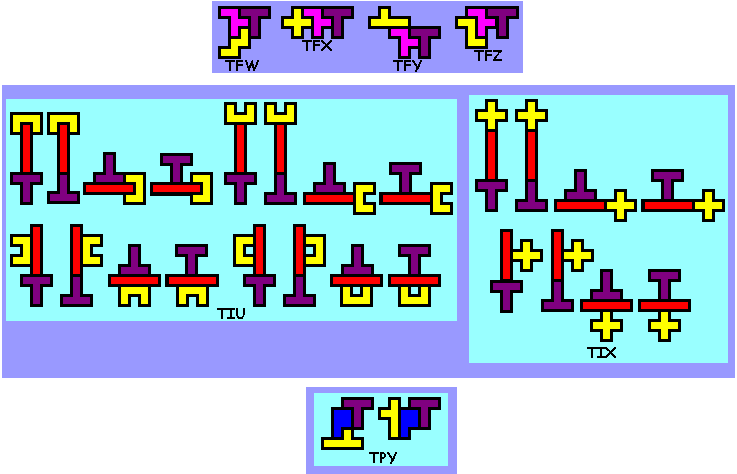
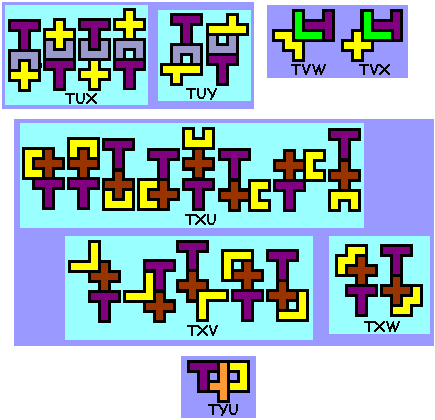
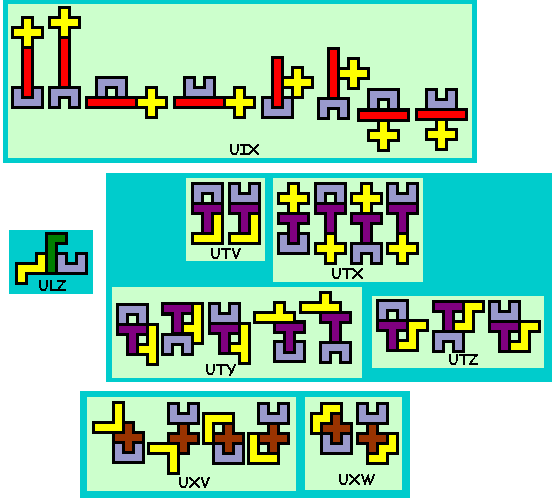
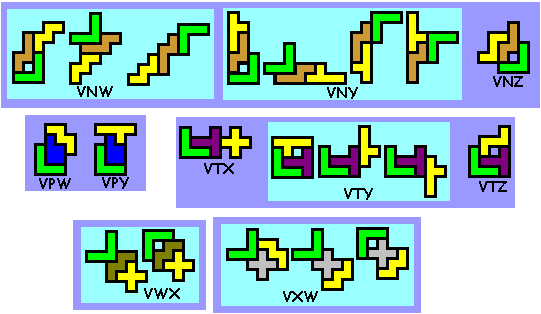
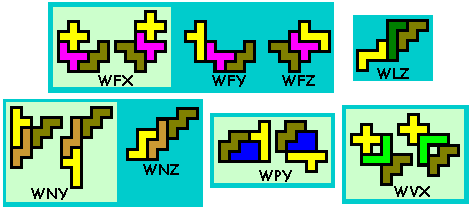
Weet je nog andere of heb je opmerkingen, graag een mail naar o.d.m@fulladsl.be