We breiden dit verder uit.
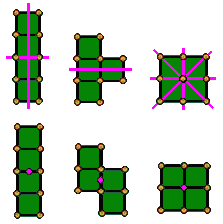
Zoek alle mogelijke figuren bestaande uit 2 tetromino's die een symmetrieas hebben.
![]()
Aad van de
Wetering stuurde ons 9 verschillende vormen.
Om alle figuren (in totaal 17) te vinden gaan we systematisch te werk. We
gaan de figuren indelen naargelang de afmetingen van de omgesloten rechthoek. Aad mailde ons alle verschillende oplossingen: er zijn er 20.
We kregen een mail van Patrick Hamlyn met de volgende bemerking: We kregen dit ook bevestigd van
Peter Esser:"I think there are no shapes with rotational symmetry, which can be made from all tetrominoes because the t-tetro is unbalanced under checkerboard coloring. With four tetros omitting the t-tetro we can't get a shape with rotational symmetry neither as a computer search showed."
Zoek alle mogelijke figuren bestaande uit 4 tetromino's die een symmetrieas hebben.
Om alle figuren (in totaal 65) te vinden gaan we systematisch te werk. We
gaan de figuren indelen naargelang de afmetingen van de omgesloten rechthoek. Aad mailde ons alle verschillende oplossingen: er zijn er 83.
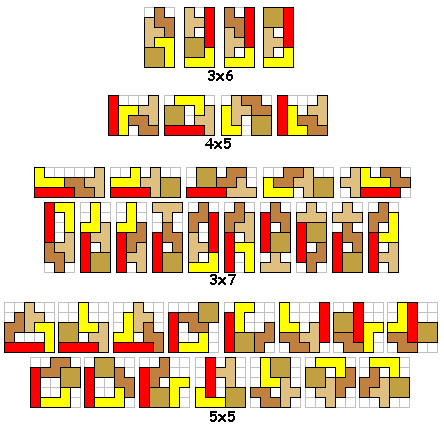
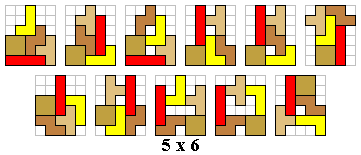
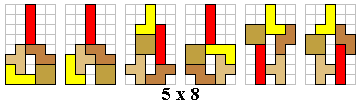
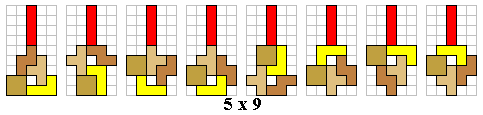
We maken met een tetrominoset alle figuren die minstens één symmetrieas hebben.
Om alle figuren (in totaal 100) te vinden gaan we systematisch te werk. We
gaan de figuren indelen naargelang de afmetingen van de omgesloten rechthoek. Aad mailde ons alle verschillende oplossingen: er zijn er 124.
We hebben de figuren, bestaande uit een tetroset, zodanig geplaatst dat ze telkens een verticale symmetrieas
hebben. Leuk is het om op te merken dat een aantal figuren een tetromino
insluiten. Brendan Owen stuurde ons op
aanvraag een animatiegifje waarbij hij uit de 100 symmetrische vormen er zes
vond die ook te maken waren met vier gelijke pentomino’s.
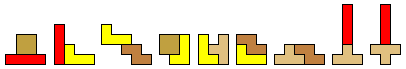
Zoek alle mogelijke figuren bestaande uit 3 tetromino's die een symmetrieas hebben.![]()
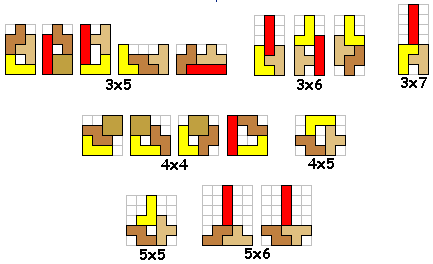
Er zijn inderdaad 3 vormen die 2 verschillende oplossingen hebben.
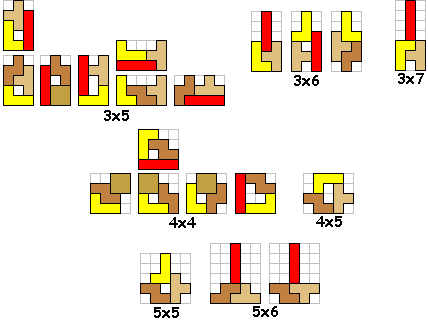
"You seem to be ignoring rotational symmetry, and considering only reflectional symmetry."
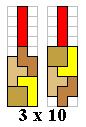
We vroegen het Aad en samen met zijn
FlatPoly2 kregen we één figuur met een symmetriemiddelpunt die gevormd werd met 3 tetromino's.

![]()
![]()
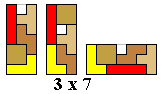
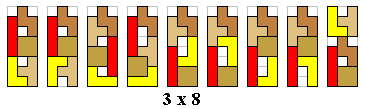
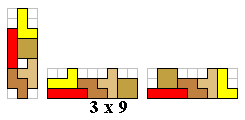
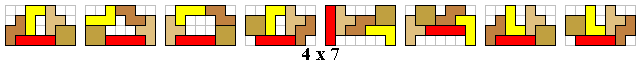
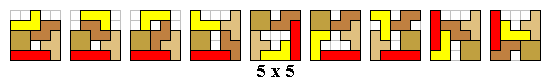

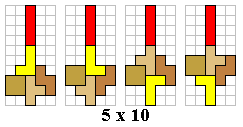
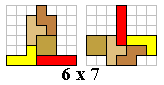
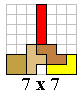
Er is geen enkele figuur te vinden met 2 of meer symmetrieassen.

Weet je nog andere figuren met een symmetrieas?
Mail het ons. Ook commentaar is welkom.
o.d.m@fulladsl.be

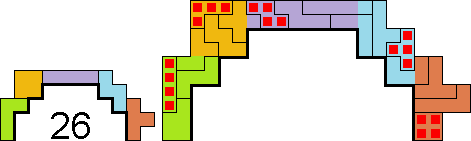
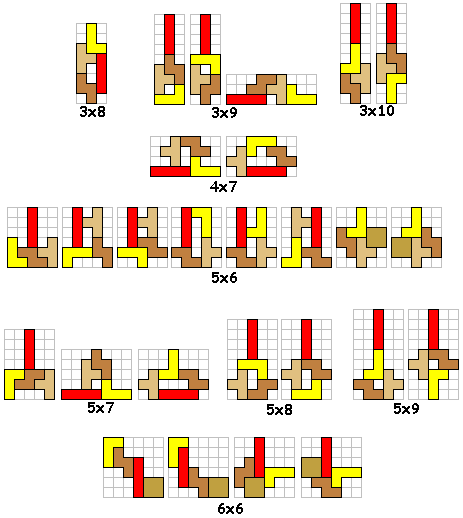
Naar aanleiding van onze tetrobrugwedstrijd (wedstrijd 43) kregen we van Edo
Timmermans een aantal leuke symmetrie-oefeningen met een set tetromino's.
Er wordt telkens een vergroting getekend op schaal 2 door gebruik te maken
van 1 tetromino- en een pentominoset.
Bij de vergroting is er geen enkel contact tussen de tetromino’s.
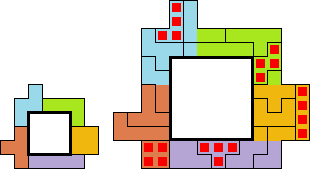
Bij alle tekeningen geldt dat binnen iedere vergrote originele tetromino een
volledige kleine tetromino ligt.
●Een zo groot mogelijk ingesloten gebied door tetromino's met symmetrische
buitenrand.
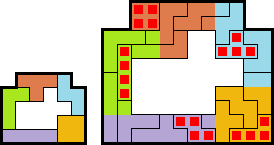
●Een zo groot mogelijk ingesloten gebied door tetromino's met symmetrische
binnenrand.
●Een zo groot mogelijk brug bestaande uit tetromino's met symmetrische
buitenrand.
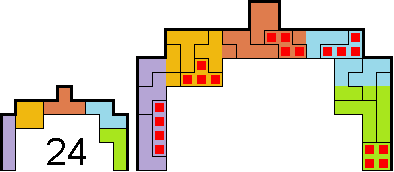
●Een zo groot mogelijk brug bestaande uit tetromino's met symmetrische
binnenrand.