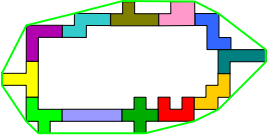
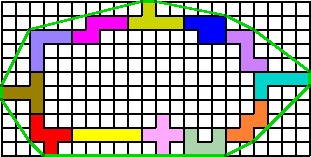
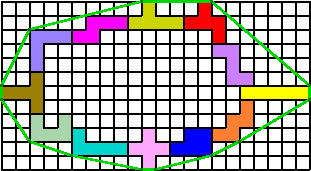
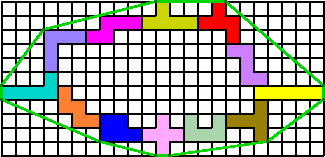
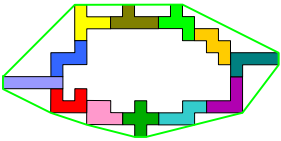
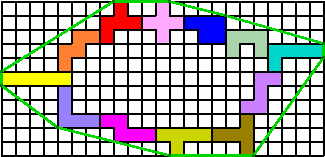
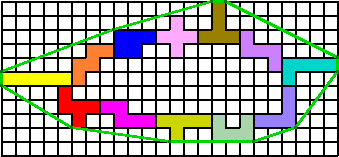
De pentomino's moeten een gesloten geheel vormen.
We spannen een touwtje ronde de roosterpunten van de set pentomino's en trekken het strak.
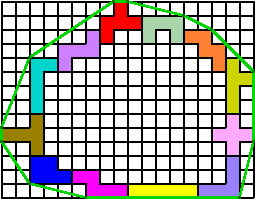
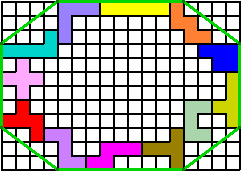
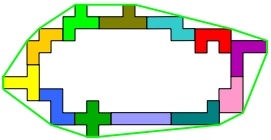
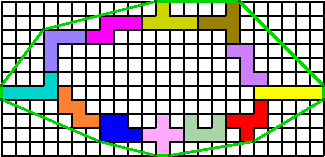
Plaats de pentomino's zodanig dat de omtrek maximaal is.
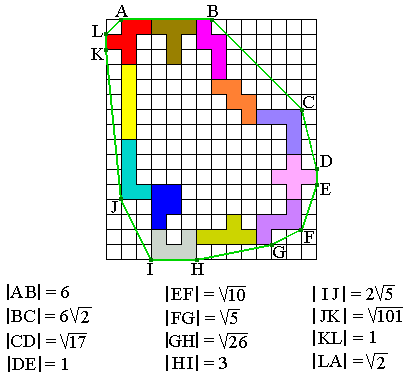
In het bovenstaande voorbeeld is de omtrek van het touw (groene lijn) 50 op 0,1 nauwkeurig.
George Sicherman (USA) stuurde 5 verschillende oplossingen.
|
|
|
|
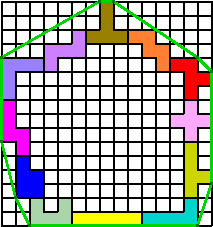
George stuurde er ook een oplossing in een rechthoek |
|
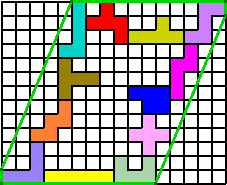
Perimeter = 50
It is easy when I use long slanted lines!
We legden het probleem voor aan Helmut.
George "You bring out the heavy artillery!"
Er ontstond een knappe competitie.
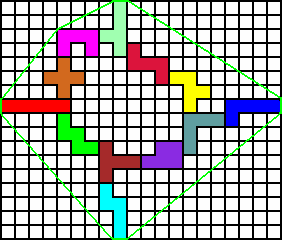
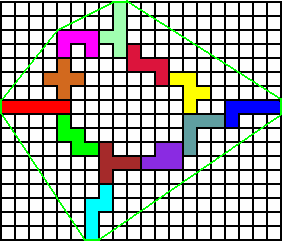
Helmut stuurde 2 oplossingen.
|
|
|
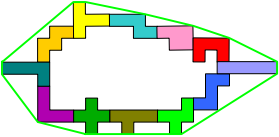
George kon dit! Hieronder zijn 4 opeenvolgende inzendingen.
|
|
|
|
|
|
Aad van de Wetering mengde zich in de competitie.
Hieronder 2 inzendingen.
|
|
|
Ik weet niet precies hoe de voorwaarden luiden, maar als alle pentomino’s in
de ring moeten dan heb ik die wet overtreden, de N en de L voldoen niet.
De pentomino's moeten een gesloten geheel vormen.
Vals gespeeld. In alle andere oplossingen ligt elke pento in de ring.
Anders zou je de X in het centrum kunnen zetten en in elk van de vier takken een
rij gestapelde pento's. Dan kan je bijna 60 halen.
Aad stuurde echter een juiste inzending:
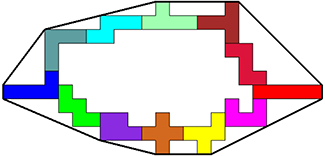
Met deze kom ik tot 54,41464327. Wel een beetje flauw, George heeft het werk
gedaan, ik kon er ietsje meer van maken door U en F te verwisselen.
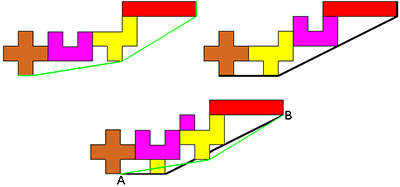
Groene weg (George) van A naar B is 11,9137
Zwarte weg (Aad) van A naar B is 11,9443
Dit is een mooie toepassing voor leerlingen op de stelling van Pythagoras.
Alhoewel Aad het zelf een beetje flauw vond, vinden wij het heel knap gezien van
Aad!
Maar... Helmut stuurde ons nog 2 oplossingen
|
|
|
Aad vond een betere oplossing, eentje met perimeter 54,5757
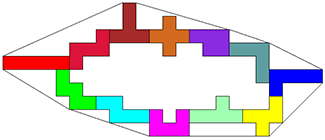
George geeft niet op en verbetert het resultaat.
|
|
|
Wie kan nog beter?
Elke oplossing is welkom
OdetteDM@outlook.com
![]()