Tetromino's en de stelling van Pythagoras

Tetromino's met een touwtje

Wie het probleem met de pentomino's te uitgebreid vindt, kan beginnen met de tetromino's.

We laten de hoekpunten van de tetromino's samenvallen met roosterpunten. De maatgetal van de zijde van een vierkantje stellen we 1. Elke tetromino moet minstens één zijde gemeenschappelijk hebben met een andere. Ze moeten dus een ketting vormen.
We spannen een touwtje ronde de roosterpunten van de set tetromino's en trekken het strak.
Plaats de tetromino's zodanig dat de omtrek maximaal is.

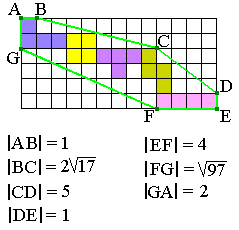
In het bovenstaande voorbeeld is de omtrek van het touw (groene lijn) 31,1 op 0,1 nauwkeurig.

Goede oplossers verwerven eeuwige roem.
Mail naar: o.d.m@fulladsl.be

Naam	Land	Oplossing
Aad van de Wetering	Nederland	34,425217879
Helmut Postl	Oostenrijk	34,4775
Peter Jeuken	Nederland	34,4775
George Sicherman	USA	34,4775

Aad van de Wetering kwam met een leuke nieuwe opgave: Plaats de tetromino's zodanig dat de omtrek minimaal is.

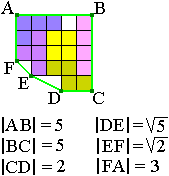
In het bovenstaande voorbeeld is de omtrek van het touw (groene lijn) 18,65 op 0,01 nauwkeurig.

Goede oplossers verwerven eeuwige roem.
Mail naar: o.d.m@fulladsl.be

Naam	Land	Oplossing
Aad van de Wetering	Nederland	17,99
Helmut Postl	Oostenrijk	17,8995
George Sicherman	USA	17,8995
Peter Jeuken	Nederland	17,8995

Peter Jeuken:"Het lukte eerst niet om hetzelfde minimum te vinden als Helmut en George. Totdat ik ontdekte dat 17,8995 gelijk is aan acht plus zeven maal wortel twee. De omtrek moest dus 8 rechte stukjes en 7 stukjes onder een hoek van 45 graden bevatten."

George Sicherman bezorgde ons nog een leuke variant.
Maak met de tetromino's een symmetrische vorm zonder gaten. Omspan met een touwtje en probeer een minimale en een maximale omtrek te vinden.
George stuurde een oplossing van min. 18,49 en max. 25,03.
Wil je de oplossing zien? (Eerst zelf zoeken.)

Kan je beter?
Mail naar: o.d.m@fulladsl.be