Records Wedstrijd 10

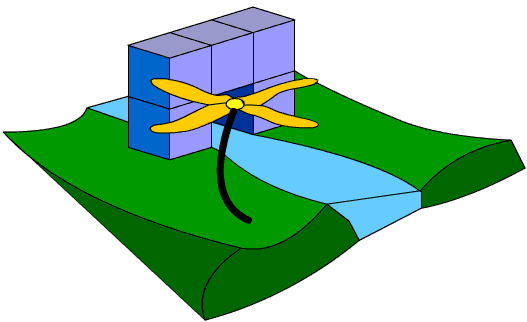
Deze tekening kregen we van onze winnaar van de symmetrische brug: Roel Huisman uit Hengelo Nederland. Hij bezit ook het record van de kleinste symmetrische brug met een binnensymmetrie.

Onze vriend Pillow uit Italië wou zo graag een symmetrische brug maken maar vond het te moeilijk en hielp ons bij het bouwen van de ingezonden oplossingen

Robert Henderson uit USA stuurde ons twee verschillende oplossingen van een symmetrische brug van 270:

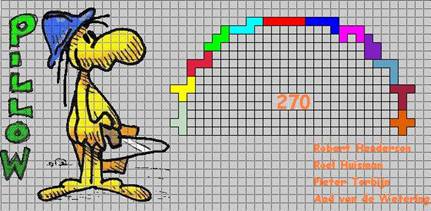
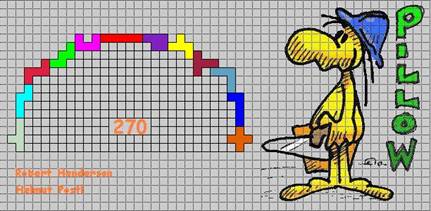
Van Roel Huisman uit Nederland kregen we als eerste de oplossing van 270. Dit schijnt een nieuw record te zijn

Ook van Pieter Torbijn uit Nederland, Helmut Postl uit Oostenrijk en Aad van de Wetering uit Nederland kregen we een oplossing maar wel dezelfde als die van Robert Henderson . Beschikken deze pentominofanaten over telepathische gaven of zouden er maar twee verschillende oplossingen zijn?

We kregen een symmetrische brug van 268 van Bob Allen uit de USA

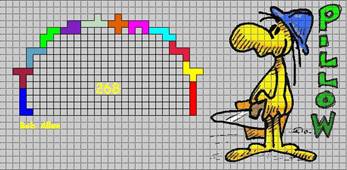
We precies dezelfde oplossing van 268 van Patricia Etcheverry uit Argentinië, Robert Henderson uit de USA,Roel Huisman uit Nederland, Brad Jansen uit de USA, Andreas Rottler uit Duitsland en Aad van de Wetering uit Nederland. Toch telepathie?

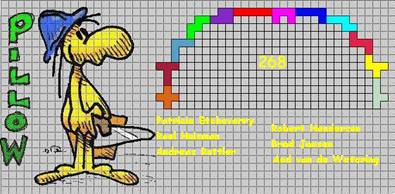
Helmut Postl uit Oostenrijk bezorgde ons ook een oplossing van 268:

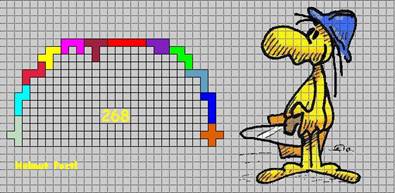
Ton Tillemans uit Zwitserland vond nog een andere oplossing van 268:

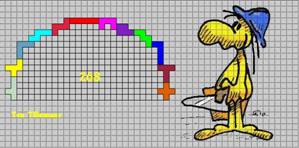
We kregen van Pieter Torbijn uit Nederland ook nog 3 verschillende symmetrische bruggen van 268.Voor oplossing 1 leek hij hulp gekregen te hebben van Patricia, Robert, Roel, Brad, Andreas of Aad. Had Helmut hem geholpen bij oplossing 2? Maar wie had hem geholpen bij oplossing 3?

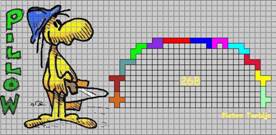
We bekeken de brugsilhouetten van 268 eens nader. Waarom kregen we zeven inzendingen van silhouet 1?

Bij dit silhouet zijn er zes verschillende oplossingen en toch kiest men met 6 (van de 7 inzendingen) voor dezelfde oplossing.

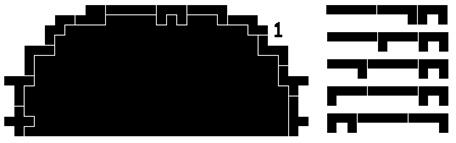
Silhouet 2 van Bob Allen heeft maar twee oplossingen.

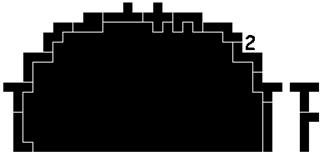
Bij de 2^de oplossing wordt de L-pentomino verticaal gespiegeld.

Silhouet 3 van Helmut Postl heeft vier oplossingen

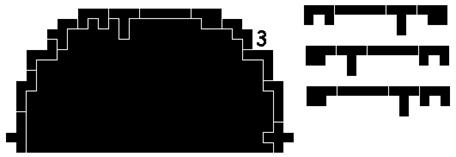
De I- en T pentomino kunnen van plaatst gewisseld worden enerzijds en anderzijds kunnen de P- en U pentomino gewisseld worden.

Het mooiste silhouet kregen we van Ton Tillemans want zijn oplossing is uniek.

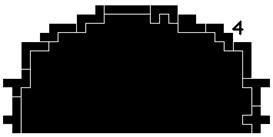
Silhouet 5 van Pieter Torbijn heeft vier oplossingen.

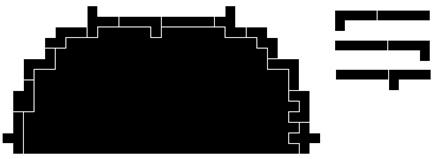
We kunnen de I- en L-pentomino van plaats wisselen en daarbij kunnen we telkens de L-pentomino spiegelen.

Patricia Etcheverry  stuurde ons ook haar andere oplossingen.Samen met haar man en haar 10-jarige zoon Maxi had ze al die symmetrische bruggen gevonden.

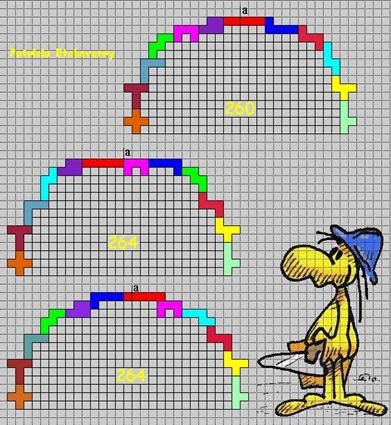
Van Ton Tillemans uit Zwitserland kregen we nog een oplossing van 263:

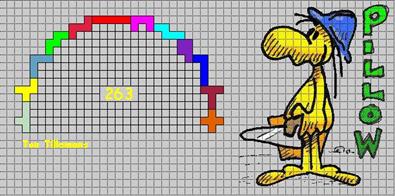
We appreciëren elke inzending want het maken van een symmetrische brug vinden we zelf lastig.

We kregen van William Waite uit Denemarken een inzending van 256.

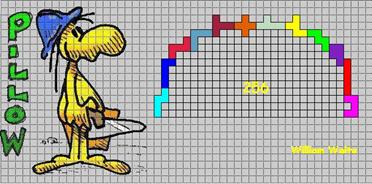
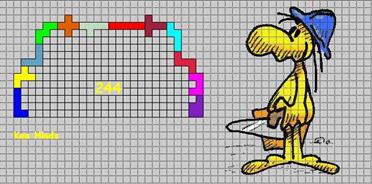
Ken Hinds uit de USA mailde ons een symmetriebrug van 244. Ons voorbeeld bij de opgave had 254 ingesloten vierkantjes.Wat was Ken zijn bedoeling? Toch vonden we het leuk om een oplossing van hem te krijgen.

Op 9 maart 2002 kregen we van Aad van de Wetering een mail waarin stond dat hij door het zoeken naar onze opgave een brug gevonden had met een binnensymmetrie van 272. Hij vroeg zich af of dit al bekend zou zijn onder de polyominologen.

Kan je dit ook of misschien nog beter mail het ons dan: