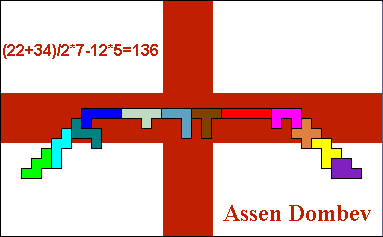
We kregen een maximale brugoplossing van 136 van:














Bob en Jürgen probeerden dit record te breken door onze voorwaarde”de ingesloten oppervlakte door de brug moet een geheel vormen” niet te respecteren.
Toch vinden we dit heel knap gevonden. Misschien een idee voor een volgende wedstrijd?


Tijdens het groepswerk over pentomino’s vonde leerlingen van het 3e jaar Elektromechanica een oplossing van 129.
Je kan het boekje
hier
downloaden.
Het is in pdf-formaat en dus te lezen met
![]()

Patrick Hamlyn mailde ons dat er 1056 oplossingen waren voor ons probleem.
Samen met Peter Esser dachten we er verder over na.
Om een maximale brug te bekomen moeten we in het horizontaal gedeelte gebruik maken van I,T V en Y We kunnen deze pento’s in willekeurige volgorde plaatsen dus zijn er 4!=1x2x3x4=24 mogelijkheden.De V- en Y-pento kunnen we op 2 verschillende manieren plaatsen, dus wordt het aantal mogelijkheden 4!x2x2=96

Klik hier om alle mogelijkheden te zien.
Alle mogelijke combinaties van 2 maal 7 trappen met de overige 8 pentomino’s:
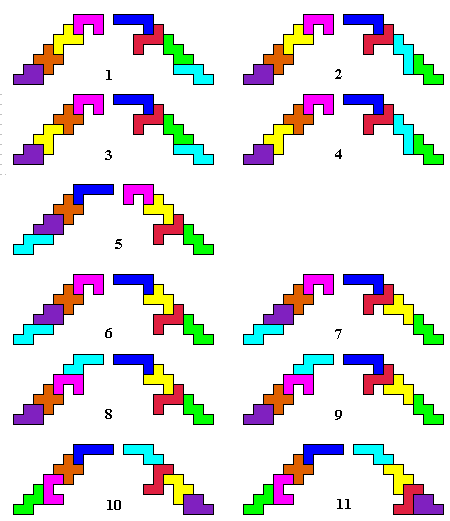
Er zijn dus 11 combinaties die we kunnen maken.
Deze verschillende combinaties vonden we dank zij FlatPoly2.
Wij vinden dus 11*96=1056 oplossingen.
We kunnen het niet laten van toch even naar de vorm van de oplossingen te kijken.
We ontdekken dan 2 keer 2 congruente brugjes.
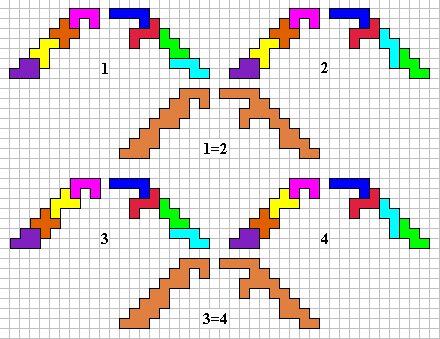
We vinden dus dat er 9x96=864 verschillende oplossingen
Aad van de Wetering sprak dit pertinent tegen:”De oplossingen met de congruentie NW en WN worden als verschillend beschouwd door de polyominologen.
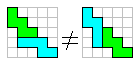
Anders zouden er geen 65 oplossingen zijn voor 8x8 met centraal gat 2x2.Dus hoe je het ook wendt of keert, er zijn 1056 oplossingen.”
Ook Patrick Hamlyn mailde ons”Heel wat oplossingen hebben dezelfde vorm, maar met de stukken anders geplaatst. Je moet dit bekijken als verschillende oplossingen, anders zou je bijvoorbeeld kunnen zeggen dat het vormen van een rechthoek van 6x10 met een pentominoset maar 1 oplossing heeft”
En toch vinden we 864 verschillende vormen!