
We danken onze vriend Pillow voor de schitterende tekening.

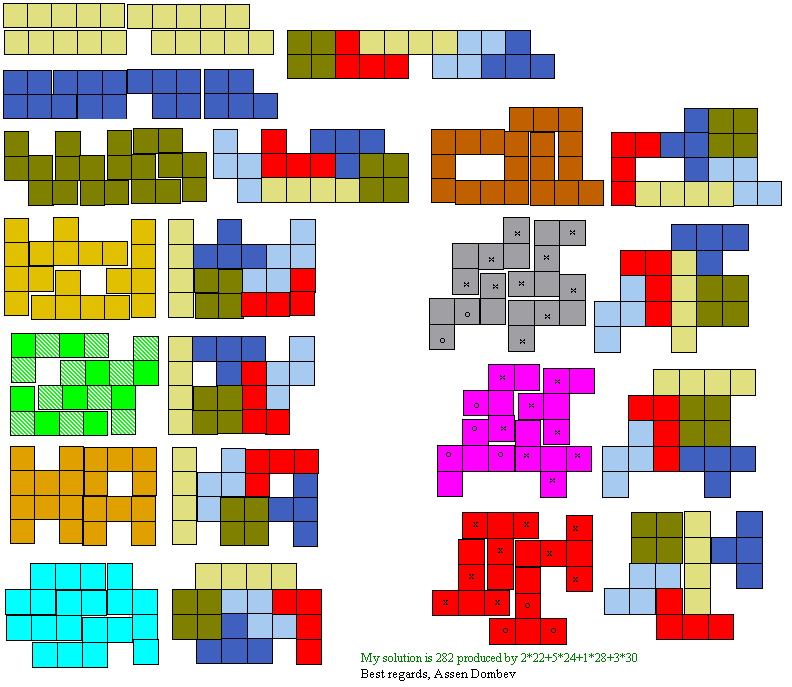
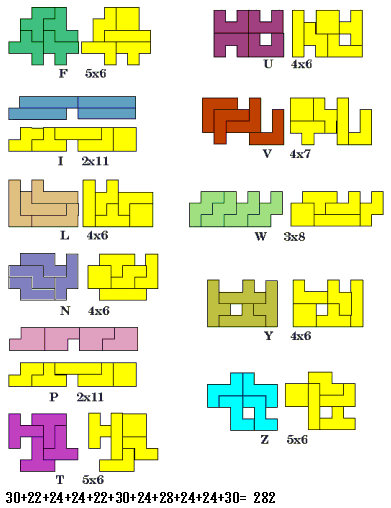
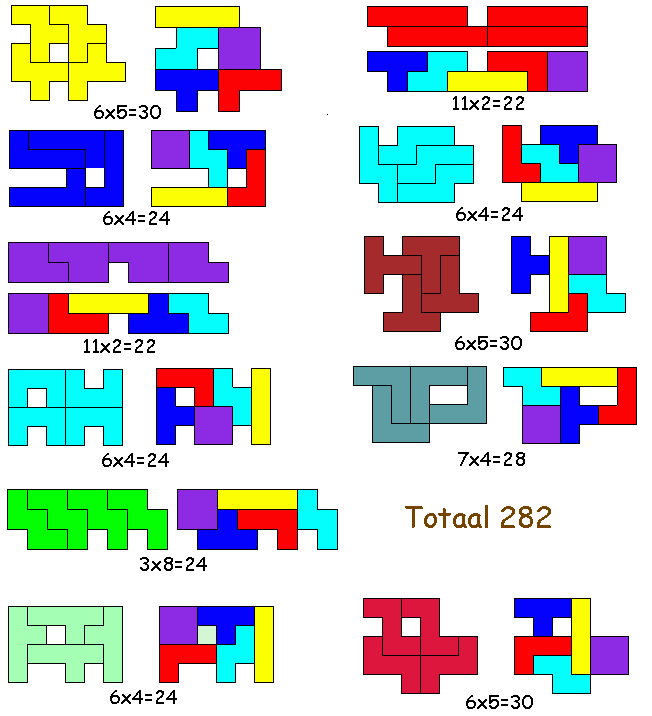
We kregen een minimale oplossing van 282 van:
Assen Dombev uit Engeland
Peter Esser uit Duitsland
Patricia Etcheverry uit Argentinië
Uit haar mail: "It was really a pleasure to play with all this figures
for a couple of weeks. Thank you.”
Patrick Hamlyn uit Australië
Hij mailde ons hoe hij de oplossing gevonden had:
“A complete search reveals the optimal solution.
Method:
1.
For each rectangle (3*7, 2*11, 4*6, 3*8, 2*12, 5*5, 2*13, 3*9, 2*14,4*7, 5*6,
4*8...) I run my solver with the five tetrominos plus enough monominos to fill
the shape. I list all the shapes found, encoding them as hexadecimal digits
(using zero for monomino else 1). Four cells make one digit, in raster order.
Each list is sorted and duplicates discarded.
2. For each pentomino, solve for the same set of
rectangles (smallest first) using four copies of the pentomino plus monominos to
fill. List the shapes found in the same hexadecimal encoding, sort & discard
duplicates.
3. Add the pentomino list to the tetromino list for
each rectangle, sort and look for matching shapes.
4. Stop looking for a pentomino as soon as a match
is found."
This
finds:
2*11 - IP
4*6 - LNUY
3*8 - W
4*7 - V
6*5 - FTZ
2*2*11 + 4*4*6 + 3*8 + 4*7 + 3*5*6 = 282
Bob Henderson uit de USA
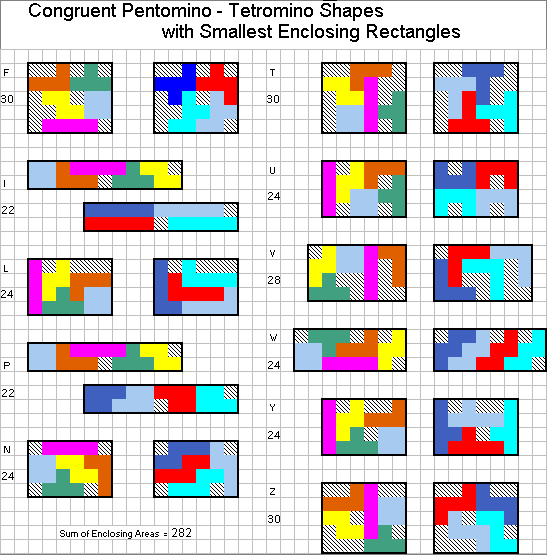
Uit zijn mail: ”Thank you for making a interesting tetromino competition
challenge! It was also kind of you to thank me for giving you the idea for this
puzzle. I hope you get many entries in your competition!”
Roel Huisman uit Nederland.
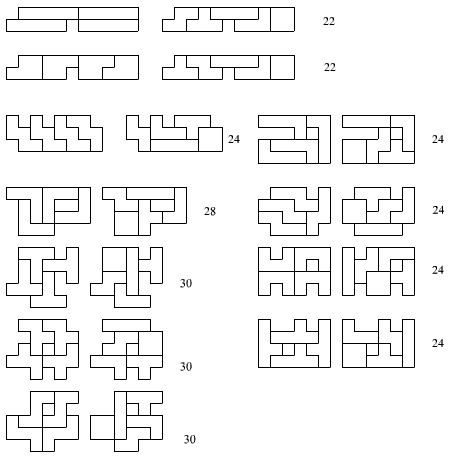
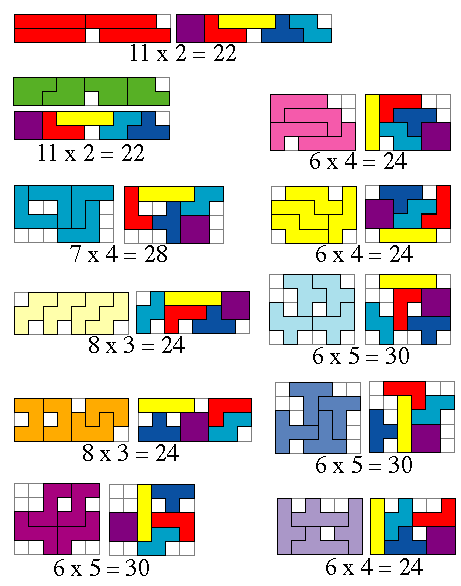
Brendan Owen uit Australië.

Brendan stuurde ons alle mogelijke oplossingen! Sommige vormen kunnen op
verschillende manieren gevuld worden met tetromino’s maar hij toont altijd maar
één oplossing:
| Pentomino | Afmetingen rechthoek | Oppervlakte | Kleur | Vorm |
| I | 11x2 | 22 | Grijs | 1 |
| P | 11x2 | 22 | Oranje | 1 |
| U | 8x3 of 6x4 | 24 | Bleekgroen | 2 |
| L | 6x4 | 24 | Geel | 6 |
| Y | 6x4 | 24 | Paars | 1 |
| N | 6x4 | 24 | Roze | 1 |
| V | 7x4 | 28 | Cyaan | 4 |
| W | 8x3 | 24 | Donker groen | 1 |
| T | 6x5 | 30 | Blauw | 1 |
| F | 10x3 of 6x5 | 30 | Groen | 30 |
| Z | 10x3 of 6x5 | 30 | Rood | 7 |
| X | geen oplossing | geen oplossing | geen oplossing | geen oplossing |
Christian Paulsen uit Denemarken
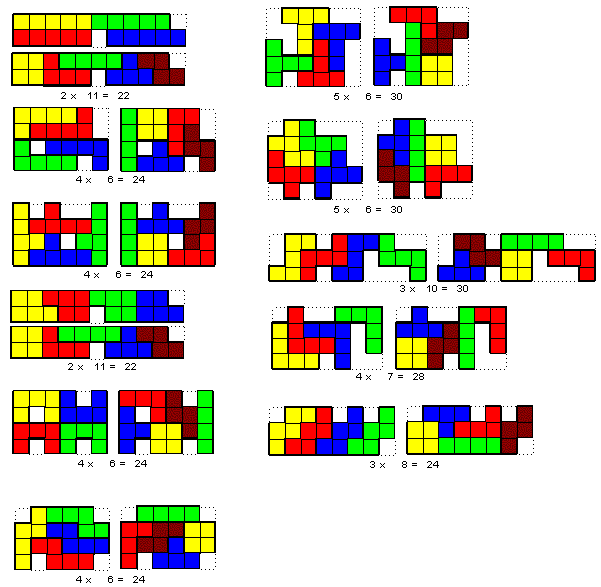
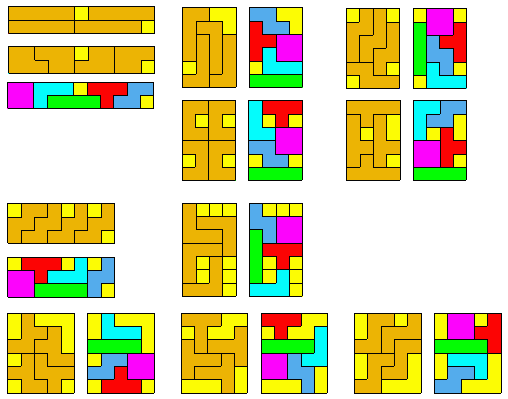
Helmut Postl uit Oostenrijk

Helmut gebruikte ons exelbestandje om zijn oplossingen te vinden en te tekenen
Uit zijn mail: ”It’s a nice Tetromino page with a clever Excel spreadsheet to
do the puzzle."
Sergio Stanzani uit Italië
Uit zijn mail: ”Congratulation for the nice problem! Best regard and ciao to
the next time!”
Pieter Torbijn uit Nederland
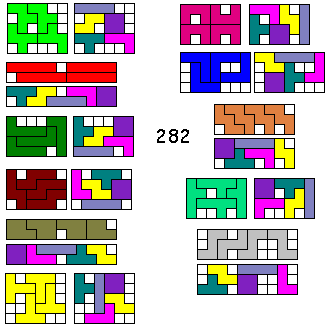
Dario Uri uit Italië
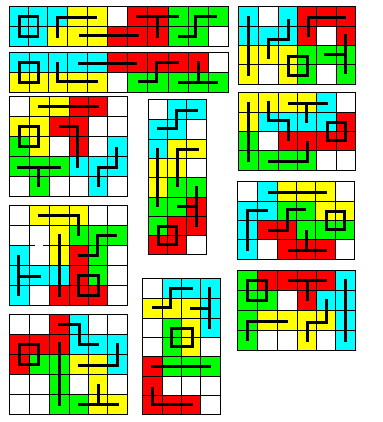
Aad van de Wetering (onze coach) uit Nederland
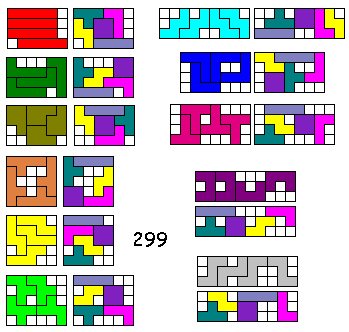
Van Ekkehard Künzell uit Duistland kregen we een oplossing van 299.
Dari Uri uit Italië gaf ons het voorstel: ”The same your problem, but with maximum area seem interesting. See a example:
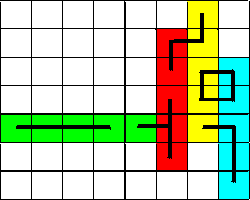
Sergio Stanzani mailde ons een oplossing voor het bovenstaande probleem:
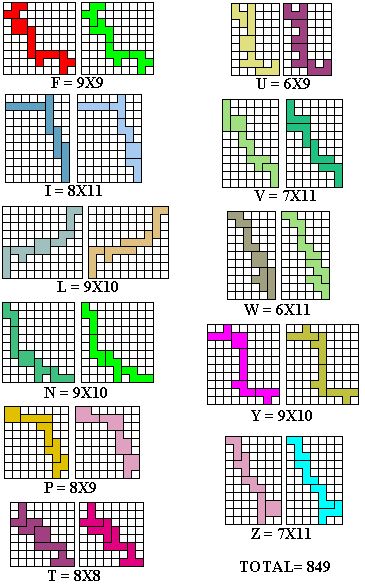
Kan je dit record 849 breken mail het ons dan.