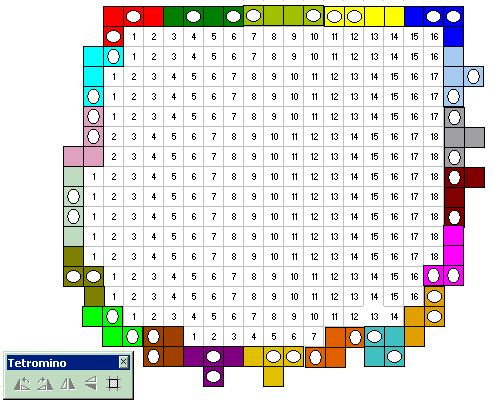
Van de volgende 'verlichte’ geesten kregen we een maximale oplossing van 273:
Peter Esser uit Eschweiler (Duitsland).

Gaël Gaytant uit Ronse (België)

Bob Henderson uit Livonia (USA)

Roel Huisman uit Hengelo (Nederland)

Helmut Postl uit Wenen (Oostenrijk)

Sergio Stanzani uit Bologna (Italië)

Ton Tillemans uit Uetendorf (Zwitserland)

Pieter Torbijn uit Den Haag (Nederland)

Aad van de Wetering uit Driebruggen (Nederland).

Pieter Torbijn stuurde als verjaardagsverrassing voor mevr. De Meulemeester een omheining van 274!!
We hadden wel ‘in de gaten’ dat het een verjaardagsgrapje was.

Van Assen Dombev uit Sofia (Bulgarijë) kregen we geen maximale oplossing maar wel een hele uitleg.
About the new competition, my result is only 268
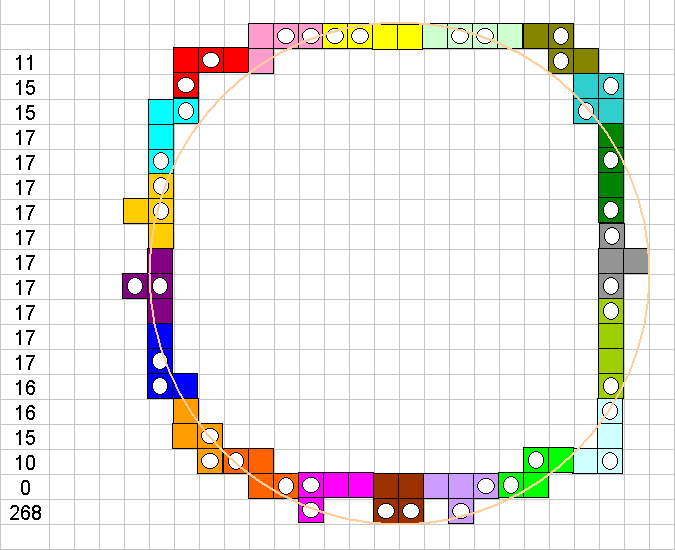
My logic was: the max length of the set is 4*4 + 14*3 + 2*2 = 62. Enclosed areas if is a rectangle 30 x 1 (31+31 = 62) = 30. If is near to square 15 x 16 = 240, if is a circle (l = 2piR) 62 = 3.14D, D = 19.7, in this case enclosed area is piR^2=3.14*9.87*9.87 = 306.
Therefore enclosed area should be a shape nearer to circle with R=10. I tried to put all items following this my rule. Without holed/unholed rule my result is 274. But here because the number of borders with holes is equal to number of borders without holes the two 2x2 items have to be put
one on line one on circle. But for max enclosed area I made (274) both 2x2 need to be on circle, what calls holes/unholes rule broken.
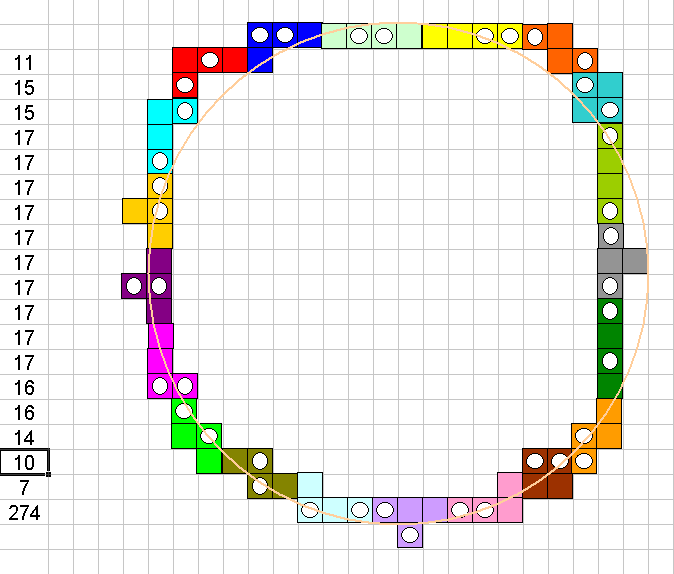
From the task I know, max is more than 268, probably 269, but I couldn't find it. Seems 274 is impossible, but I have not enough strong proof for this. Anyway, I am waiting for the next competition.
Jonah DeWall uit Philadelphia, USA mailed ons een oplossing van 280 maar hij was onze voorwaarde:” De vierkantjes van de verschillende tetromino’s die elkaar raken moeten beide ofwel een gaatje hebben, ofwel geen gaatje hebben.” vergeten.
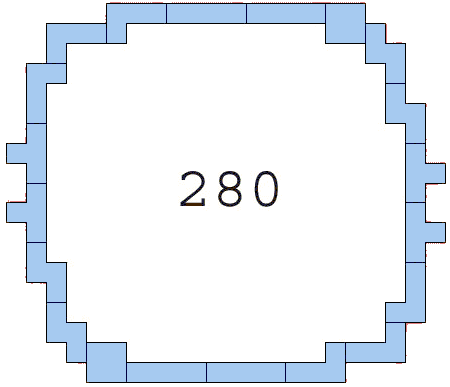
Zou dit een maximale oplossing zijn indien we de voorwaarde “De vierkantjes van de verschillende tetromino’s die elkaar raken moeten beide ofwel een gaatje hebben, ofwel geen gaatje hebben” weglaten?
Ook Michael Keller uit USA deed ons bijna geloven dat hij een recordverbetering had.Hij stuurde ons een oplossing van 276. Zie je waar het fout gaat? Onze wedstrijd was deze keer nogal moeilijk om maximale oplossingen te vinden. Van Rakefet Kol uit Haifa (ISRAEL) kregen we volgende mail: Onze leukste bedrieger was echter Ted Lakerveld uit Rotterdam (Nederland). Op 27 oktober 2002 ontvingen we een volgende mail: En wij maar tellen...
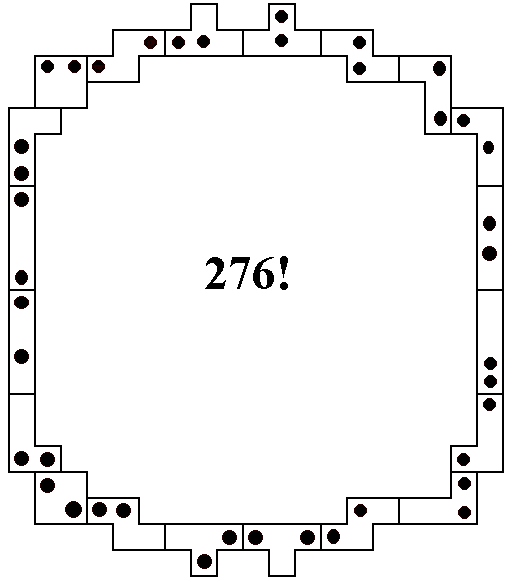
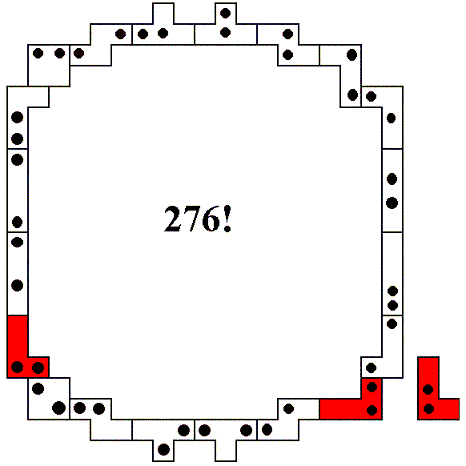
We zijn echter blij met elke ingestuurde oplossing.
We kregen een oplossing van 271 van Patricia Etcheverry uit Buenos Aires (Argentina)
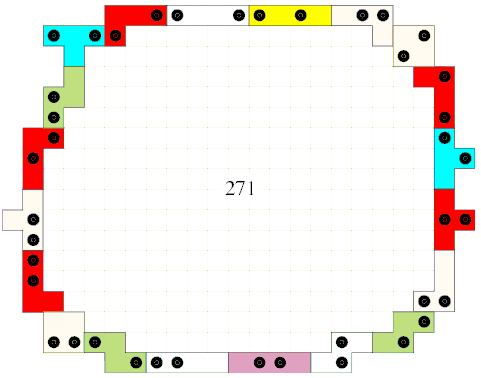
”My current solution is 263, so I guess I'm still away from winning your competition... but at least I'll get a tetromino set ;-)”
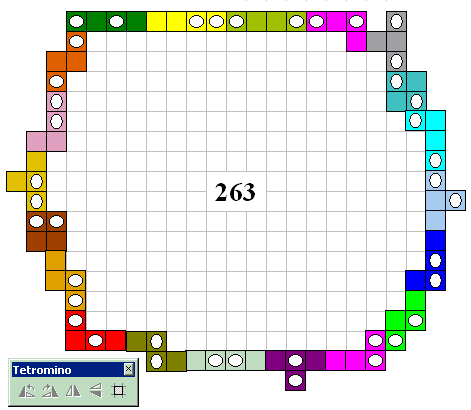
Op 26 oktober 2002 ontvingen we een mail:
“Een regen- en stormachtige zaterdag is het ideale moment om achter de computer te gaan zitten en een puzzel op te lossen. Wat heet echter oplossen: ik ben niet verder gekomen dan 260 vierkantjes H"et is wel echt "handwerk", schuiven met de onderdeeltjes over je scherm. Oplossingen vinden met behulp van de computer vind ik nog steeds niet leuk.”
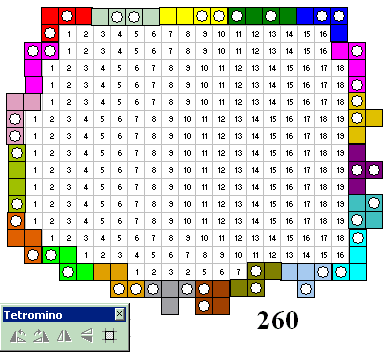
“Het stormt buiten, dus goed weer om nog eens te puzzelen.
Het is een marginale verbetering, maar ik heb het toch tot 262 vierkantjes gebracht.”