
Deze wedstrijd leek heel moeilijk.
Een heel dikke proficiat aan degenen die toch een maximale oplossing van 122 gevonden hebben:
| Naam | Land |
| Gabriele Carelli | ItaliŽ |
| Bart De Worm | BelgiŽ |
| Bob Henderson | USA |
| Helmut Postl | Oostenrijk |
| Pieter Torbijn | Nederland |
| Aad van de Wetering | Nederland |
Dit zijn de 2 silhouetten van de oplossingen van 122 die we toegestuurd kregen.
Zouden er nog andere zijn ?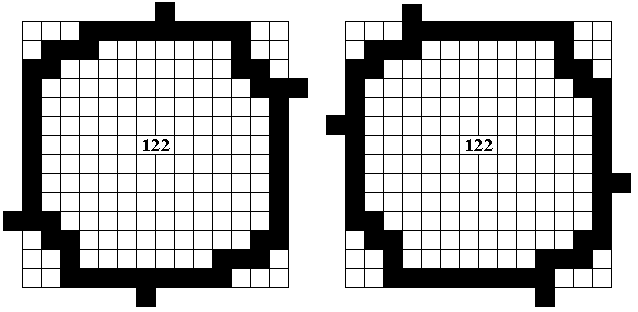
De moeilijkheidsgraad van onze wedstrijd blijkt nog meer uit het feit dat zelfs onze beste deelnemers eerst minder goede oplossingen stuurden.
Bij zijn verschillende oplossingen mailde Aad van de Wetering ons:"128 is het maximum voor een fence. Er 18 inleveren voor een scheve symmetrie is nogal wat. Toch liggen alle pentokes behoorlijk efficiŽnt en 't heeft bijna iets weg van een cirkel.
Nu al 116, waar gaat dat heen?
Het gaat maar door, nu al op 120. En de U-pento zou nog beter moeten kunnen, wie weet.
Nog een verbetering van mijn record, van 120 naar 122. Wie weet kan het nůg beter..."
We denken het niet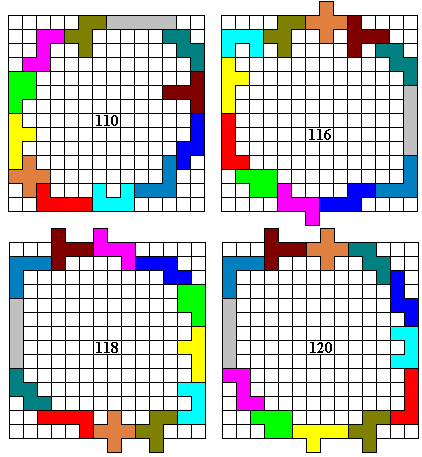
En Bob Henderson mailde:"Here is my first solution to your latest pentomino competition. I am sure that better solutions are possible. Thank you for sharing this interesting puzzle!
This was a difficult challenge to solve without the assistance of computer logic, but I have also found a solution enclosing an area of 122 units. If I find any better results by the end of the month I will let you know!"
We denken dat het niet beter kan.
En van onze befaamde Helmut Postl:"For the new contest, I found an area of 116. I'm rather sure that this is max, but not quite. So it's interesting what the others will have found."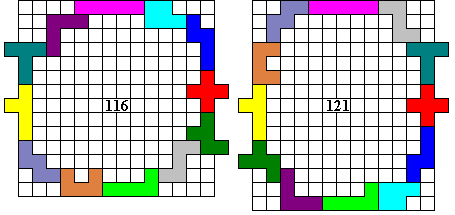
When you told me about Aad's area 122 I thought that this cannot be true. But it is true! Don't ask me why I didn't come even close to it earlier (so about 120) - maybe I didn't invest very much time into it... Well, here is my new solution with area 122, too. But with 'help' from Aad, since I knew the area already. Great, Aad!"
De oplossing van 121 stuurde Helmut ons toe op aanvraag. De ingesloten oppervlakte kan dus ook een oneven aantal vierkantjes zijn!
Omdat we deze wedstrijd zo moeilijk vonden, vermelden we de andere inzendingen.
We zijn er ook heel blij mee!
MichaŽl Dowle uit Engeland had bijna het record.
Sasha Ravsky uit Rusland maakte ook een omheining van 120.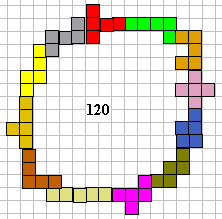
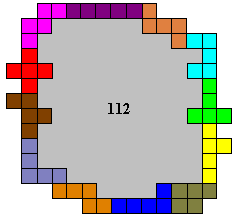
Ken Hind uit USA mailde:"So far I have been able to find an answer with interior space of 112 units. I think maybe I can do better, but I will send you this answer now.
This is an enjoyable contest."
Peter Sipos uit Hongarije stuurde een oplossing van 111.

Johan Viljoen uit Zuid Afrika mailde:"I am pretty certain this is not the maximal solution, but time constraints preclude me from searching further. Or maybe as a cricket supporter I had to stop when I reached the Nelson 111. I found several of size 111, of which one example is attached."
In het 3de jaar probeerden de leerlingen een omheining te maken met een symmetriemiddelpunt.
Voor sommigen was het reeds moeilijk om een juiste oplossing te vinden.
We probeerden samen de oplossingen te verbeteren door sommige pento's te spiegelen.
Heel dikwijls werden de omheiningen beter door ze even breed als lang te maken.
We merkten op dat een rechthoek met dezelfde omtrek de grootste oppervlakte heeft als hij een vierkant is.
Hier volgen een aantal omheiningen:
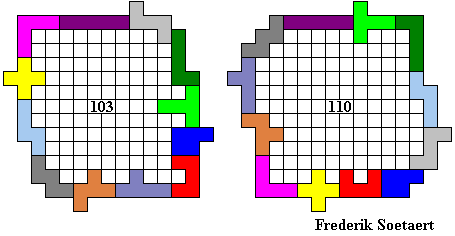
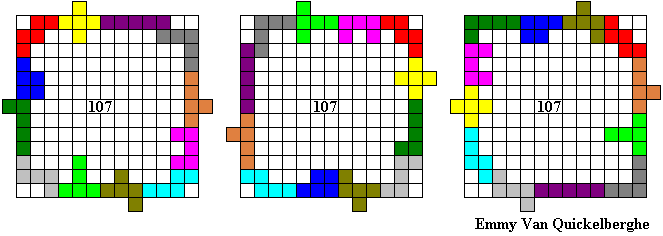
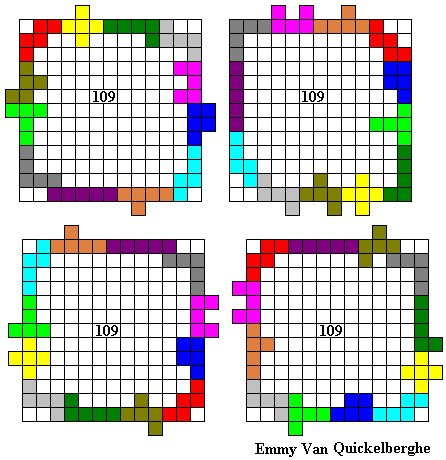
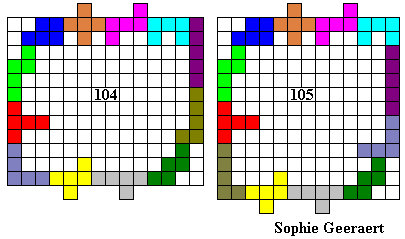
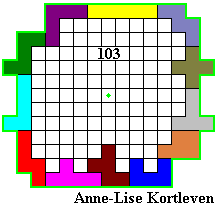
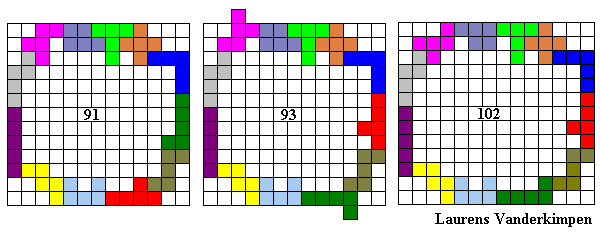
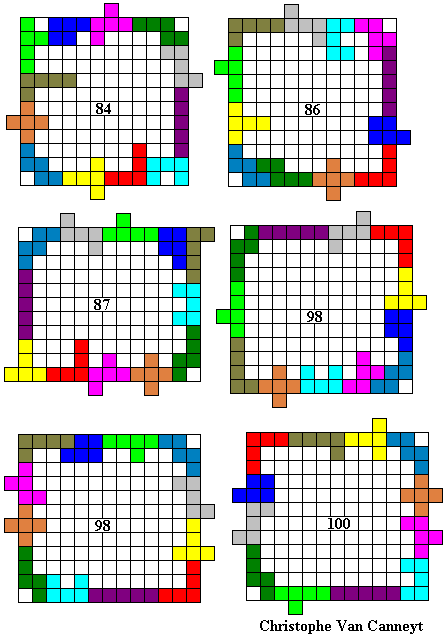
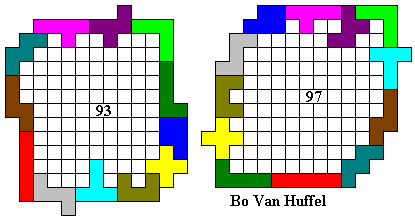
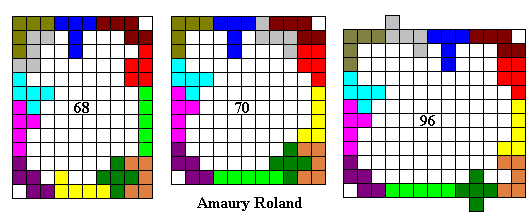
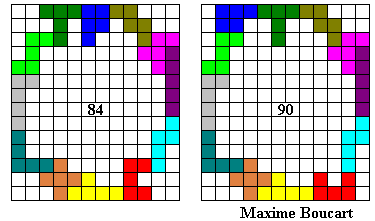
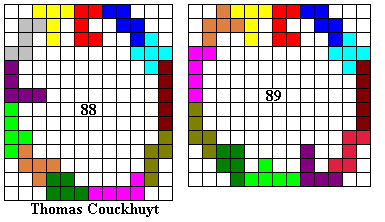
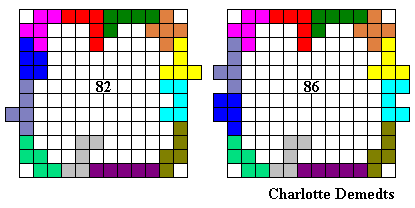
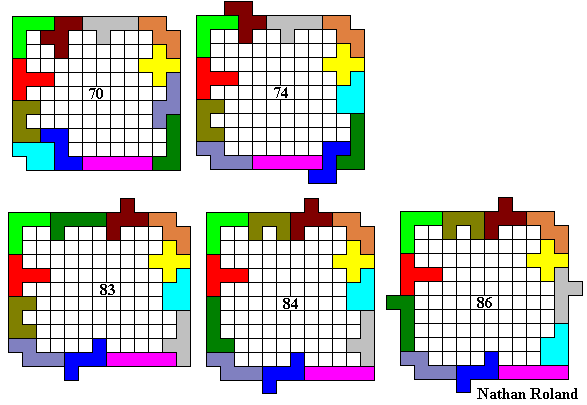
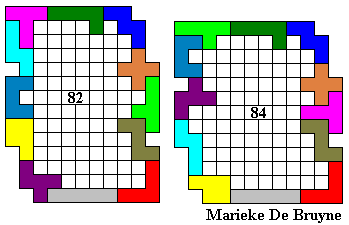
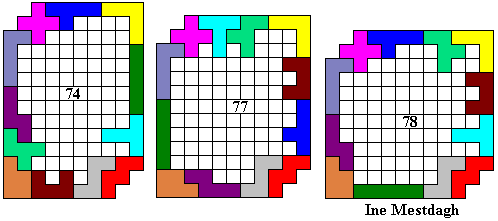
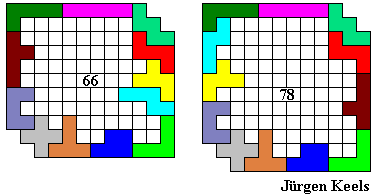
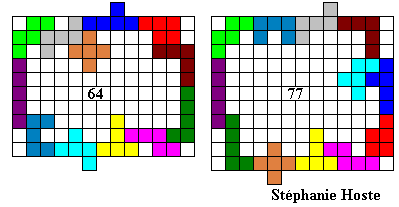
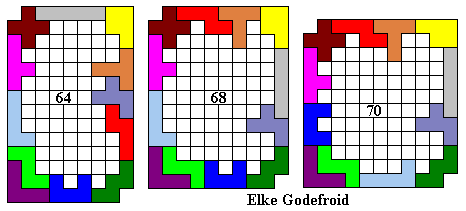
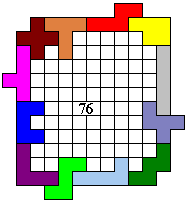
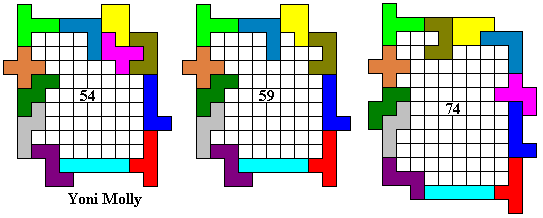
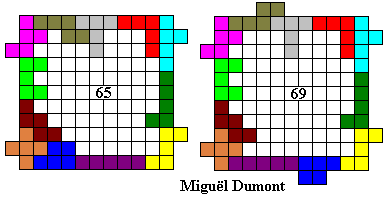
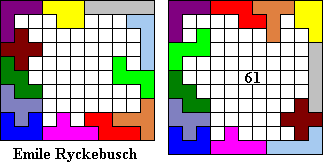
Emile maakte de grootste omheining waarvan de buitenomtrek een rechthoek is (vierkant).
Deze voorwaarde is echter niet noodzakelijk omdat de figuur een symmetriemiddelpunt zou bezitten.
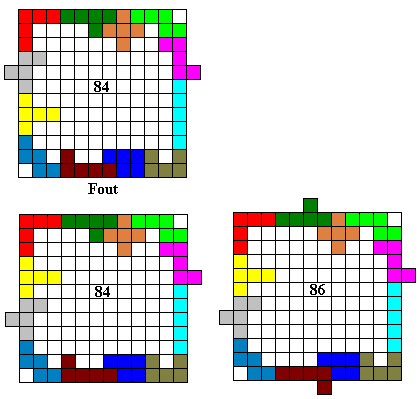
Iemand maakte een omheining met een symmetrieas i.p.v. een symmetriemiddelpunt.
De fout was echter vlug hersteld.
Bij vaststelling van fouten of onvolledigheid, mail
naar:
