Bijdrage van elke pentomino voor het vormen van de buitenomtrek van de
rechthoek
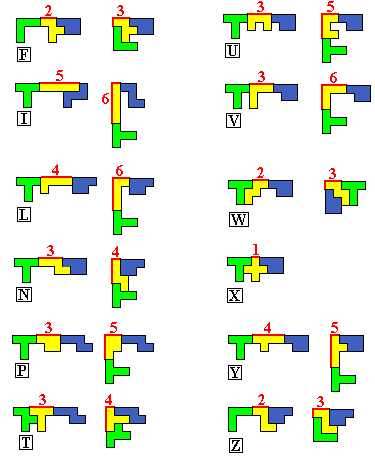
We zien dat de beste keuze
leidt tot het beschikken over 6+6+5+4+3+3=27 eenheden
Hiermee moet onze ingesloten rechthoek een
maximale oppervlakte bezitten.
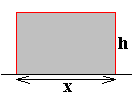
x + 2h = 27 => h = (27 - x) : 2
Opp. rechthoek= f(x) = x.h
f(x)=x(13,5 -0,5x)
f(x)=-0,5x²+13,5x
Zoek waar deze functie haar maximum heeft.
Je kan hiervoor je
TI84 Plus gebruiken (als je er geen hebt
kan je er één winnen)
Neem bv. als window-instellingen:
Xmin=-30; Xmax=30;Xscl=5; Ymin=-100;Ymax=100; Yscl=10
Je vindt voor de x-waarde van de top 13,5=>h=6,75
We denken dus dat er een maximale oppervlakte zal bereikt worden als x=13 en
h=7.
We maakten ook een
exelfile.
![]()