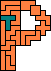This contest is dedicated
to Pieter Torbijn, who turned 80
on the 10th of December.
You have one set of pentominoes and one set of tetrominoes:
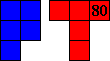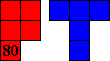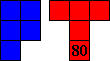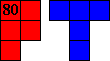
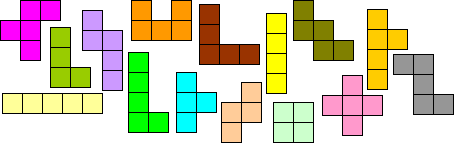
In total they have 80 squares;
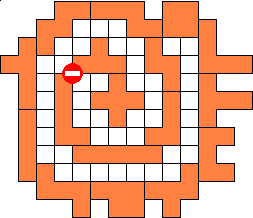
use these to make the longest narrow corridor.
The path must be one square wide all the way.
The path must be completely enclosed by pentos or tetros that share at least
one edge.
The pentominoes and tetrominoes must lie in a plane.
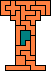
In our example the path length is 44 units.
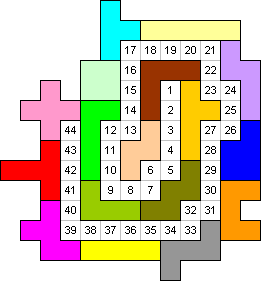
|
 |
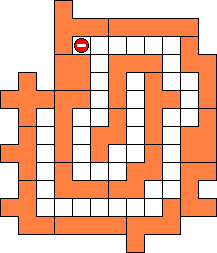
Not allowed for
the corridor:
|
 |
|
|
(point) contact with
itself |
branches |
|
 |
 |
|
This Excel file
will make searching
for a solution a bit easier.
To download it click with the right mouse button and choose ‘Save target as
...’ to save this Excel file on your hard disk or diskette.
An help in
searching for solutions is the program “FlatPoly2”. You can download it from
the homepage of Aad van de Wetering, Driebruggen.


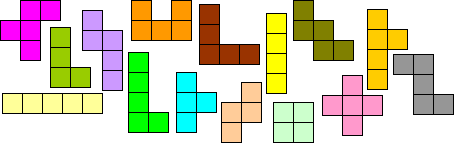


![]()