Records Wedstrijd 28

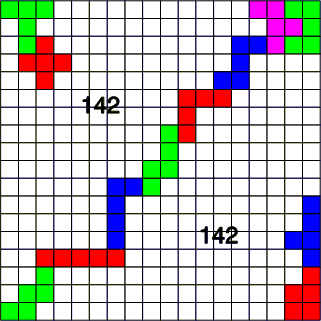
We dachten Pieter Torbijn een koekje van eigen deeg te geven, maar onze poging mislukte.
We geven hier een overzicht van hoe ons probleem aangepakt werd door Aad van de Wetering.
"Eerst de maximale lengte van elke pentomino inventariseren: 3 – 5 – 4 – 4 – 3 – 3 – 3 – 3 – 3 – 3 – 4 – 3, samen is dat 41. En dat is jammer, want er moeten 3 lijnen worden gemaakt. Maar ja, je kunt de pentokes niet uitrekken, dus moet de hoogte van de rechthoek 13 zijn, de breedte mag van jou niet verder dan 16 gaan"
Laurence Derycke vond op die manier een oplossing van 74 in een rechthoek van 16x13.

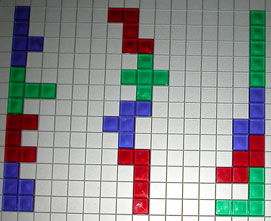
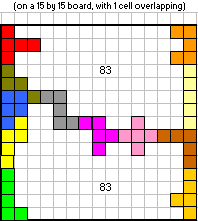
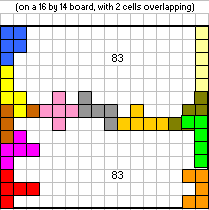
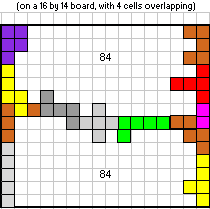
En Aad mailde:"Jouw resultaat is groter dan 74? Maar (13 x 16 - 60) / 2 = 74 en ik heb uitgerekend dat je niet naar een hoogte van 14 kunt. Sinds wanneer kan jij toveren?" en later: "Nu heb ik het wel helemaal door… 'k Heb nu een oplossing in een ruimte van 14x16. Een ruimte van 15x15 (oneven) kan niet en 15x16 lukt me net niet, één te weinig."
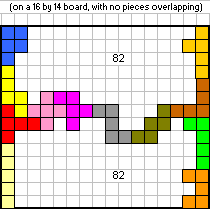
Dit is de oplossing van Thomas Van Renterghem van 82 lege vakjes.

Maar er kwam nog beter, en Aad mailde weer:"Als je veel met die pentokes speelt raak je kennelijk gedeformeerd, je wilt ze zo veel mogelijk aansluiten, of mooie groepjes vormen. Maar het is waar, zo kan het ook, er is niets tegenin te brengen, al had je het zo zeker niet bedoeld. Misschien moet je toch eisen dat alle stukjes een geheel moeten vormen, dus geen eilandjes her en der."
We hadden het inderdaad niet zo bedoeld, maar we moesten het goedkeuren.
Dit is Laurence Derycke haar oplossing van 98.

De meeste variaties ontvingen van Daan Juttmann die het echter niet vertrouwde of het wel juist was. (We hadden het inderdaad niet zo bedoeld.)

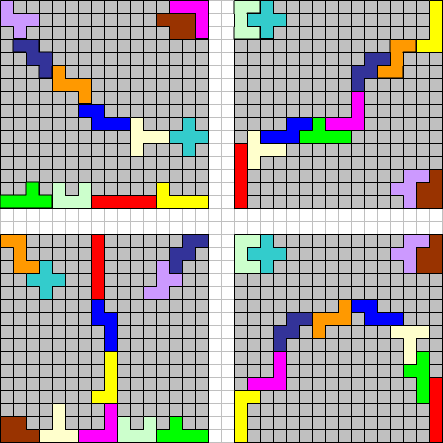
Zijn mail:"Leuk weer een nieuwe opdracht te hebben - maar toch lijkt deze toch iets te gemakkelijk te gaan. Ik heb een aantal oplossingen gevonden (opp: 2x 98) die allemaal aan de voorwaarden voldoen, maar ze lijken niet op het voorbeeld dat op de site gegeven is. Het voorbeeld suggereert dat het moet gaan om drie stroken pentomino's - twee langs de randen en een door het midden - maar dit staat verder niet in de regels. In ieder geval zijn deze oplossingen maximaal, omdat de rechthoek niet groter mag zijn dan 16x16. Dit zijn slechts een paar van de vele mogelijkheden.
Overigens heb Ik ook mijn maximale oplossing bijgevoegd die wel op het voorbeeld lijkt (opp: 2x 74).
Mocht ik de opdracht toch verkeerd begrepen hebben, dan puzzel ik graag nog even door."

Bob Henderson dacht er niet aan van 2 pento's afzonderlijk te plaatsen maar hij dacht als enige aan het overlappen van stukken en kwam op die manier zelfs tot 84. Hij mailde:"I'm sure that most of your competitors figured out that the fence that divides the rectangle into 2 pieces can be longer (allowing a larger rectangle) if it connects the pentominos that fill the sides of the rectangle rather than the unoccupied sides as shown in your example. My first result shows how this allows the use of a of 16 by 14 unit rectangle with an area of 16 * 14 = 224, less 60 units of area for the 12 pentominos = 164, divided into just 2 equal parts gives an area of 82 units for each part that is not covered by the pentominos.

At first I thought that a 15 by 15 rectangle could give a slightly better result, but this gave an odd number of units for the area to be split. I wondered how I could make this area even, and soon realized that the open area would be one unit larger if the pentominos could overlap by one unit! This gave 2 equal open areas of 83 units for a 15 by 15 rectangle or for a 16 by 14 rectangle with 2 overlapping pentomino squares.

Finally, I found a way to overlap 4 of the pentomino squares on a 16 by 14 rectangle, leaving 2 open areas of 84 units each. Each pentomino covers 5 squares of the rectangle, but 4 of the squares are covered by more than one pentomino. I hope that this is allowed by the rules! If not, the 82 unit solution for no overlap is my best result."

Dit zijn onze andere deelnemers :
(voor hun oplossing te zien, klik op hun naam)
 

Naam	Land	Aantal
Benoît Boucart	België	Afgekeurd98
Gabriele Carelli	Italië	74 98
Marco Carelli	Italië	74
Laurence Derycke	België	74
Nils De Meue	België	98
Patricia Etcheverry	Argentinië	74
Peter Hendriks	Nederland	Afgekeurd73
Tom Jolly	USA	98
Daan Juttmann	Nederland	74 98
Michael Keller	USA	74 82
Helmut Postl	Oostenrijk	98
Sasha Ravski	Oekraïne	74
Kenneth Saey	België	82 Afgekeurd 93 Afgekeurd 94 98
Edo Timmerman	Nederland	74 Afgekeurd
Leon van den Broek	Nederland	74
Aad van de Wetering	Nederland	74 82 98
Berend Jan van der Zwaag	Nederland	82 98
Stijn Van Lancker	België	Afgekeurd98 98
Johan Viljoen	Zuid-Afrika	82
Maarten Wemel	België	74 82

Helmut Postl bracht een nieuwe opgave aan:"There's a fine trick with the new contest to achieve the absolute maximum, namely the 16x16-square. This gives an area of 98 for each of the two regions. If the condition of the maximum for the sidelengths is relaxed - for example, look for the biggest square (not rectangle, since they can be arbitrarily big!), a sidelength of 18 is even possible (gives area 132)."

We kregen reeds een oplossing van Tom Jolly, maar hij is dan ook de winnaar van deze wedstrijd.
Hij kan goed puzzelen maar schijnbaar niet rekenen ;-)


Bij vaststelling van fouten of onvolledigheid, mail naar: