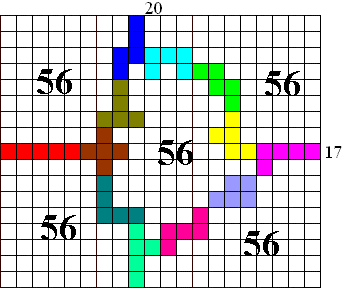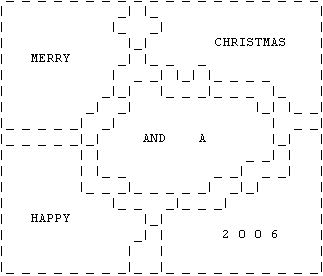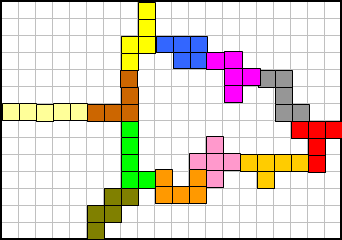Records Wedstrijd 29
Toen Edo de wedstrijdopgave voorstelde had hij ook nog een aantal andere opgaven die terug te vinden zijn bij opdrachten op onze site.
Hij ondertekende zijn opgave op zo'n leuke manier dat we daarmee onze records willen beginnen.

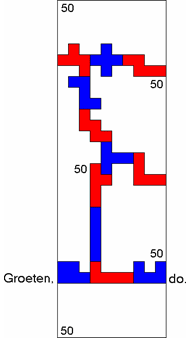
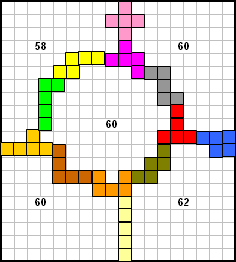
Deze oplossing voldoet niet aan onze wedstrijd want er stond als voorwaarde:"met een door pentomino’s omsloten ruimte in het midden".
Esther Pluess en Berend Jan van der Zwaag stuurden een gelijkaardige oplossing in.
We geven hieronder een overzicht van het zoekproces van Aad van de Wetering.
Voorlopig lukt het met 51. Misschien kan 16 x 20?

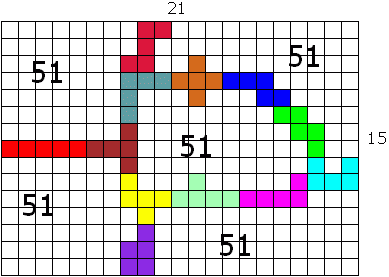
Net vond ik 52

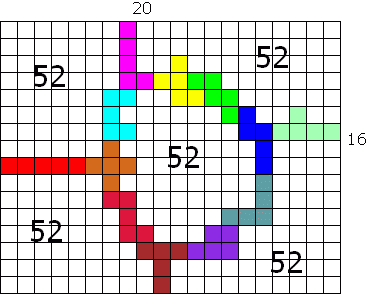
Zou dat het maximum zijn? Of zou 56 (17 x 20) kunnen?

Hoed je voor de slimmeriken:

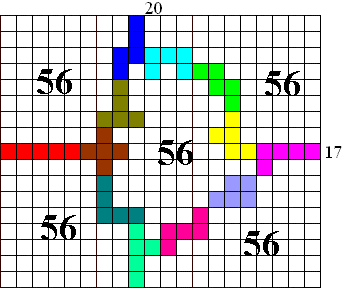
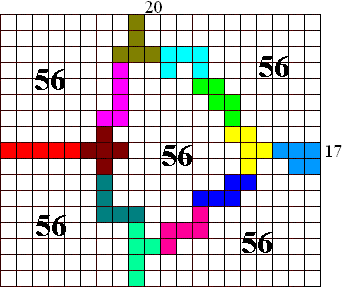
Het kan toch:

En ... ik vond er nu ook een! Als het moet gaat het beter kennelijk…

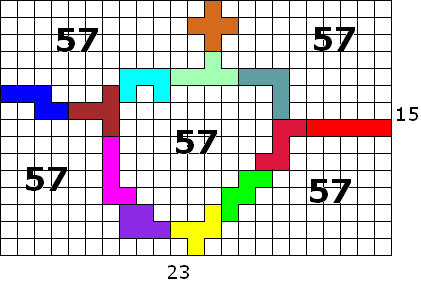
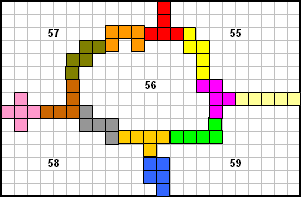
De eerste oplossing van 57 kregen we van Bob Henderson

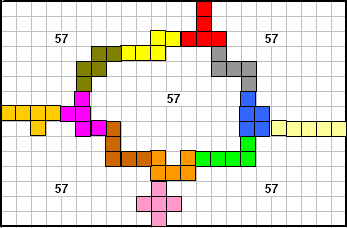
Eerst deed Bob echter ook een aantal pogingen:"My best result for the rectangle division puzzle is shown in the attached Excel file: a 17 by 20 rectangle can be divided evenly into 5 areas of 56 units by a fence made of the 12 pentominos. It may also be possible to divide a 15 by 23 rectangle into 5 areas of 57 units each or even an 18 by 20 rectangle into 5 areas of 60 units each, but I have not been able to find good solutions for these rectangles."
 

Dat het een moeilijke wedstrijd was om het maximum te halen getuigen de woorden van Helmut Postl (wie meestal alles met pentomino's spelenderwijs oplost)
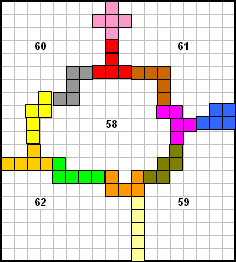
"I decided several times not to invest still more time into the 57-problem, because it took already very much time - I didn't count the hours. But finally I got it!!! I still don't believe it! I counted the areas three and four times, either to check if it's really ok and to enjoy it finding out that it's ok. Well, this problem is finished now!!! I will sleep well tonight. :-) And since I've already holidays, I don't mind the current time all too much."


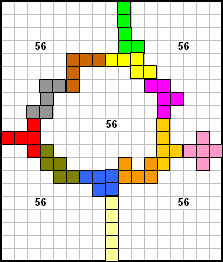
Ook Berend Jan van der Zwaag stuurde eerst een oplossing van 56 om er nadien 57 van te maken, maar misschien wou hij ons in elke taal nieuwjaar wensen ;-)




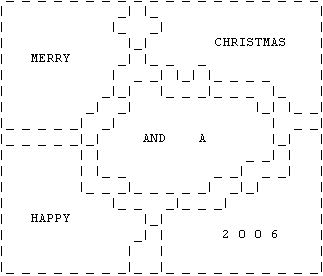
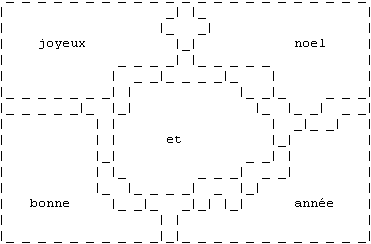
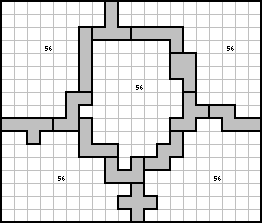
Daan Juttmann stuurde ons 2 verschillende oplossingen van 56. Uit zijn mail:"Op de valreep stuur ik nog mijn maximale oplossingen voor de ansichtkaartenwedstrijd.Was leuk om er aan te werken - ik kom tot een oppervlakte van 56 per gebied.Het is wel duidelijk dat een van de zijden van het vierkant een vijfvoud moet zijn. Voor een betere oplossing zou een 25x14, 20x18 of 15x23 rechthoek de meeste kans maken,maar ik heb er geen kunnen vinden."
 

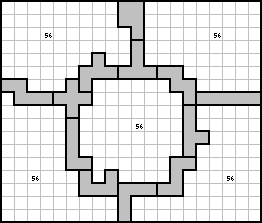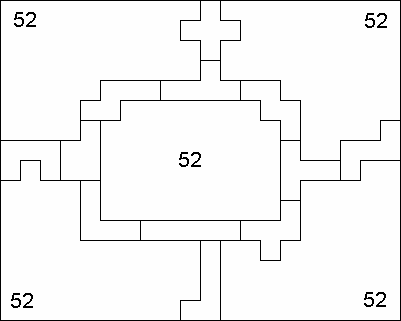
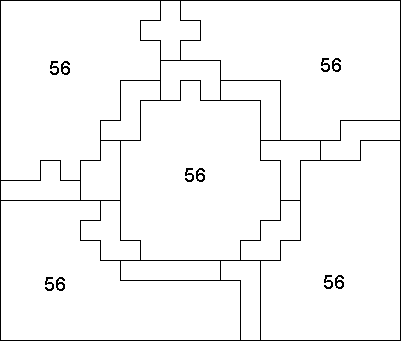
Edo Timmermans stuurde ons eerst een oplossing van 52 en verbeterde die tot 56.

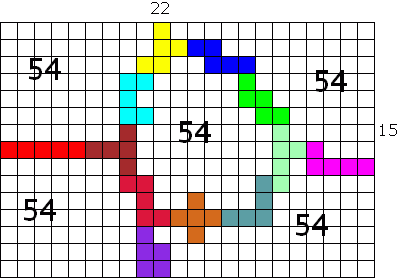
Van onze winnaar Joseph De Vincentis kregen we een oplossing van 54.
"Here is my best solution, 5 regions of area 54 in a 15x22 (area 330) rectangle"

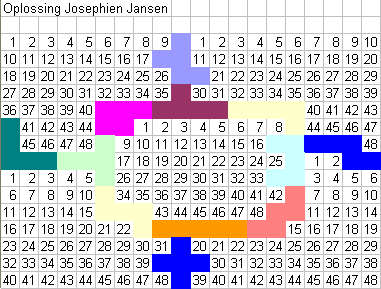
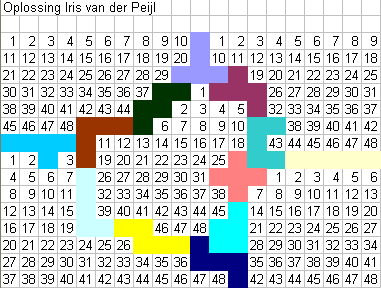
We waren heel blij met de mail van Floor van Lamoen uit het St Willibrordcollege te Goes, (Nederland). "Ik heb weer een aantal leerlingen aan het puzzelen gekregen. Drie deden het beter dan het voorbeeld. In het bestand twee oplossingen met 48 (Josephien Jansen en Iris van der Peijl) en een van 45 (Tessa de Koster)."

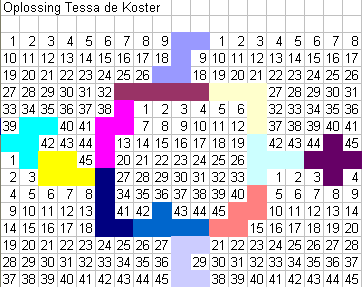
Als beloning stuurden we hun een snoep-pento-sudoku toe.
Weet je niet wat een pento-sudoku is ga dan eens op de site verder kijken.

Voor het eerst kregen we ook een inzending uit Griekenland van Ioannis Tsiamantanis.
Elk gebied had 44 vakjes.

Bij vaststelling van fouten of onvolledigheid, mail naar: