Records Wedstrijd 30
We kregen een aantal verontschuldigingen van mensen die geen tijd hebben.
Livio Zucca
"Oh my dear! Sorry, sorry, sorry. It's a long time that I'm not using the computer and my email-box is full.I hope I will soon return into the cyberspace.Good holidays! Ciao!"
Hij hield woord: kijk maar bij records 31.
Sasha Ravsky
"I'm very sorry for the delay with the answer. I have a lot of work now. The main part of my present work is the preparation of the Lviv team for the Ukrainian Mathematical Olympiad. May be I shall have more time later."
Lia Bergmans
"Het is me toch niet zo duidelijk!!!Deze wedstrijd gaat aan mijn neus voorbij...............heb nu ook weinig tijd, want ik vertrek donderdag naar Finland voor een cursus voor mijn werk, waardoor het nu nog druk is om alles af te werken..............groetjes..............."
Greetje van Dijk
"Het ligt echt niet aan de leuke wedstrijden of aan jullie superenthousiaste manier van aanprijzen! Ik kom nu niet aan spelletjes toe. Toch lacht het leven me wel toe!"
Ton en Esther Tilleman-Pluess
"Jammer waren niet thuis...Volgende keer beter"
Als je bij de volgende records kijkt zie je dat dit klopt.
Hugo Verlinde
"Ondertussen zijn er een aantal zaken veranderd voor mij. Gedaan met ict-coördinator, ik werd tot directeur aangesteld in één van de scholen van Menen. Dit betekent niet dat jullie werk mij niet meer interesseert. Ik denk wel dat ik of te laat was voor de opgave waarvan je in je mail sprak of ik heb niet goed gekeken. Wel zou ik graag blijven meedoen. Daarom vraag ik je om mij nog eens goed door te geven waar ik de volgende opgave kan vinden, welke het is en tegen wanneer het binnen moet. Dan geef ik dit wel door aan de passende leerkrachten."
Tony Sager
"Work has been very busy here as well as home life (school, family). I’ve been busy also with different web page projects in my spare time and I hope everything slows down some soon. I will try to get involved with the next puzzle when it comes out."
Ook hij hield woord
Dion Gijswijt
"Dit weekend had ik helaas niet veel tijd, maar het lijkt me een leuke puzzel. Zo gauw zie ik geen pad van lengte 50, en 63 is wel bijzonder veel! Wel zie ik in de gegeven configuratie op de webpagina een pad van lengte 47..."
Jan Kok
"Ik heb nog niets beters kunnen vinden en wil ook niet met al te slechte resultaten naar voren komen."
Tom Jolly
"I like solving the puzzles, but often I just don't have time to do them. I'm preparing a batch of game designs for a convention next month, so I've been putting aside all the 'fun' things I normally like to do, like puzzles."
Patricia Etcheverry
"Thank you for taking the time to alert me on the new competition. Unfortunately I am on exams on these weeks, so I think that my participation is quite unlikely this time. I will try to resume my participation on next competition. See you then :))"
Maar ze schatte het fout in want de volgende wedstrijd mailde ze:"Luckily the exams are over, but that doesn't mean that I have free time again, as I'm taking a couple of courses on the new semester. That means that it is very difficult for me to enter on your nice competitions. Miss the puzzles, for sure, but currently I am quite busy with house keeping, child and faculty. I have no chance, sorry. Let's see what happens on next months."
Kate Jones
"I’m sorry that I haven’t had time to work on puzzles lately. My work takes 20 hours a day. It’s a very nice competition question. I just have too many other priorities these days. I do hope in the future to get a chance to solve one of your challenges again. I attach a Valentine for you."

We hopen inderdaad dat Kate nog eens één van onze winnaars wordt.

We vroegen ons af wat maximaal zou kunnen bereikt worden.
Er zijn 8x8 inwendige snijpunten waarvan er 2 niet kunnen bereikt worden (zie op de tekening de rode punten).

Er zijn dus maximaal 63 verbindingslijntjes mogelijk.
Zelfs met de hulp van de computer scheen onze wedstrijd helemaal niet gemakkelijk.
Toch kregen we van Helmut Postl een oplossing binnen.
"Still no new result! I didn't have time the last two weeks, I had to play on balls, concerts and the corresponding rehearsals (you know, now there is the ballroom season in Vienna), and I have to improve my computer program, otherwise it will run for days and weeks (as it did already before without finding something)."
"It was good to be patient... :-) Finally I got a 63-path. I improved my computer program, and so it found a solution in a few hours."

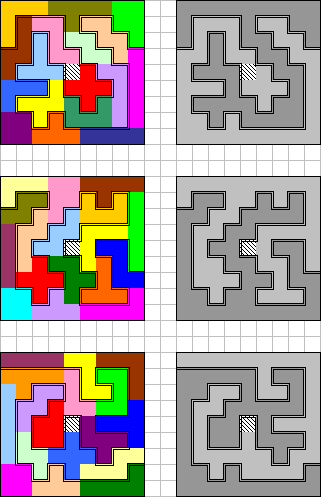
Ook Bob Henderson schakelde de computer in
"I have enjoyed the challenge of teaching my home computer how to solve your new pentomino path competition. Some of my best results so far are shown in the attached Excel file. Unfortunately, there are so many possible arrangements of the 12 pentominoes and 5 tetrominoes in the 9X9 square that my solver program may never find the best possible result!
Thanks again"



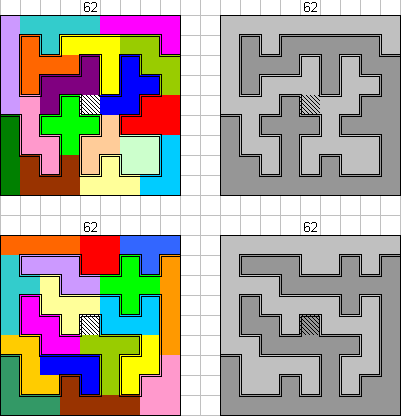
61


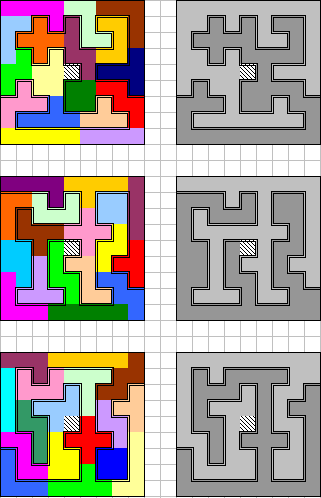
 "My computer solver program has also found 2 solutions of 62 units path length, as shown in the attached Excel file. I found the first one after telling the computer to put the longer pieces on the edges of the square (I see now that Helmut also used this method to find his solution on the 8X8 square).

The next solution of 62 units came more quickly after I also told the computer not to place any pieces where they would cause the path to have a "dead end" near the edge of the board. Since one lattice point inside the 9X9 square is not on the path in each of these solutions, it may still be possible to find a longer path. As Helmut noted, the P pentomino and square tetromino each contain an inaccessible lattice point, so that 8 * 8 - 2 = 62 interior lattice points are accessible. This gives a maximum possible path length of 63 units to connect them to each other and the sides of the 9X9 square.
 Thanks for providing this good challenge!"


"I think that you might like to see my solutions for the maximal path lengths for 8 by 10, 8 by 8, and 10 by 8 boards as shown in the attached Excel file. My program found all of these in the last few days."
We zijn inderdaad geinteresseerd. We tonen alleen de pentomino-oplossing.

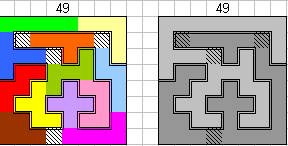
We verklappen wel dat Bob in 8x10 en 10x8 een pad gevonden heeft van 62. Het wordt misschien wel een van de volgende wedstrijden.

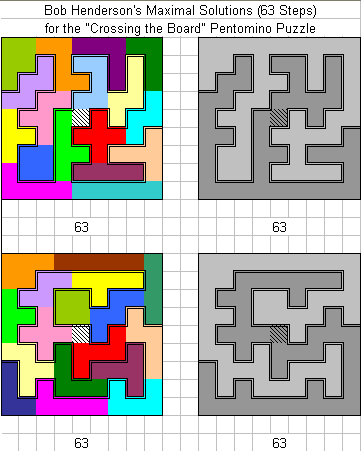
"I have good news! There was a bug in my program that caused it to miss many of the possible paths to a maximum length solution for your "Crossing the Board" puzzle. As soon as I had corrected this problem, it found a solution with a path length of 63 units! Please see the attached Excel file for this result. I was surprised that my program had earlier found so many other good answers, but not this one. . . I had already found 20 solutions of 62 units path length using the partial search (which was much faster) and had expected that it would give me one result of 63 for every 4 or 5 results of path length 62 units. Apparently I was mistaken!
Thanks for another good contest!"

 

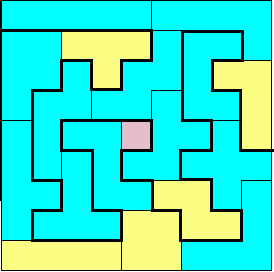
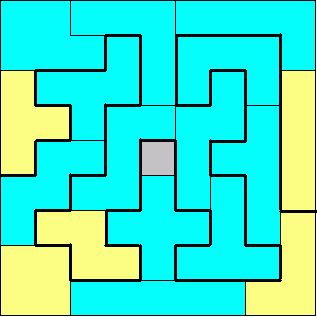
Aad van de Wetering had deze keer niet het optimum maar toch bijna.
Hij vertelde ons zijn werkwijze:"Ik liet FP ‘gunstige’ oplossingen genereren, die ik naar een bestand schreef. Daarna berekende ik met een speciaal programmaatje het langst voorkomende pad. Bij een nieuw record bewerkte ik de oplossing met Paint."
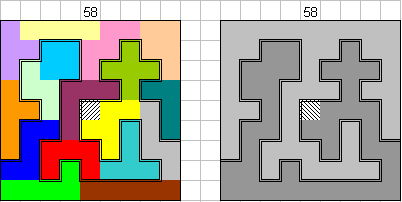
Hij stuurde ons eerst een oplossing van 61 , nadien een verbetering van 62.

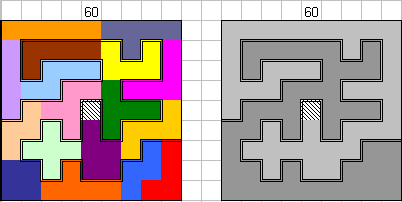
Onze winnaar Brendan Owen uit Australië begon met 58.
"I had a shot at the problem today and 63 was too hard, but I did get up too 58."

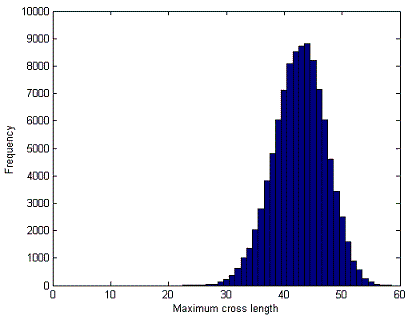
"My computer is going to do another search I will see if I can get longer then 58. Also if you are interested here is a histogram of the maximum cross length of the 100000 solutions I checked. It might be interesting to your class."

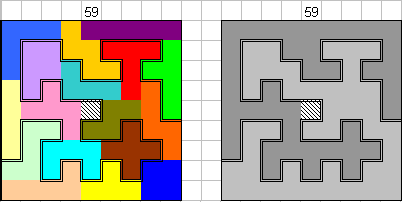
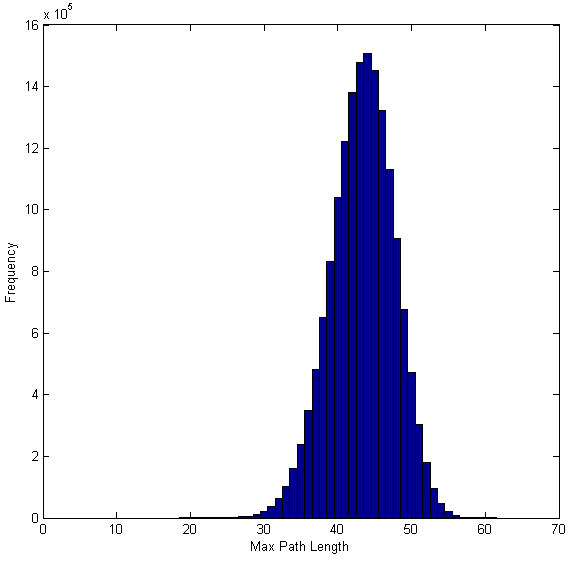
"I got 61 done. I will let you know if I get any higher."

"If you are interested I searched 16226464 different puzzle solutions and found the maximum path length for each one. Here is a frequency table of each maximum path length. I found 8 with a path length of 61."

18    0	19   10	20  23	21   15	22  52	23  155
24  395	25  893	26  1759	27  3525	28  6369	28  6369
29  12217	30  22079	31  38302	32  64196	33  102438	34  160310
35  237944	36  347622	37  480524	38  650498	39  833783	40  1039743
41  1221862	42  1381706	43  1479863	44  1507751	45  1453922	46  1323866
47  1132321	48  907573	49  677498	50  473479	51  304974	52  180842
53  97104	54  48113	55  20486	56  8310	57  2804	58  909
59  183	60  38	61  8	62  0

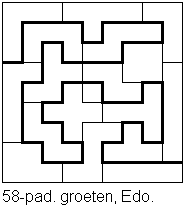
Edo Timmermans stuurde ons een oplossing van 58.
"Het is een erg lastig probleem, met dat 9*9 vierkant, om een optimale oplossing handmatig te vinden. Mogelijk probeer ik dat nog eens met de computer. Voorlopig houd ik het bij de 58 oplossing die ik vandaag gevonden heb"


Stefano Popovski vond oorspronkelijk onze wedstrijd maar niets:
"However I don't see much the point of your new problem as a brain exercise. Will explain... There is a program which accepts combined sets (in this case pentos and tetros). The tiling of the proposed surfice is solvable in minutes on a fast computer. I mean all possible solutions. This way the only problem left, is to count the path in each and it's more to be an arbiter, than to solve actual problem. Everybody can do it, still it's boring and useless. My advice is to revise a bit the problem, discuss it with the students too, there is no challenge."
Hij veranderde waarschijnlijk van mening want we kregen een oplossing van 56 binnen; alhoewel dat ze betwistbaar is volgens onze mening op het punt:"Furthermore, if you cut the board along the path, it will fall apart into exactly two pieces."



Voor het vinden van een gunstig veld was FlatPoly een uitstekende hulp.
Michael Dowle stuurde een oplossing van 54. Hij duidde heel mooi beide delen aan waarin het veld verdeeld wordt.
"My 'best' solution is attached - I feel there is a better solution but, as yet, I cannot find it."


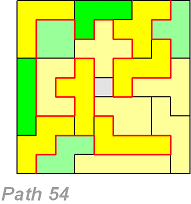
Stijn Van Lancker uit 3EE van KSO Glorieux Ronse vond 54
"Ik weet niet of ik zal winnen, maar deelnemen is belangrijker dan winnen zeggen ze altijd."
Jawel Stijn maar winnen is leuker ;-)


Maaike Kock uit Asse België stuurde ons een oplossing van 53

Ook Johan de Ruiter stuurde ons bij zijn 2de poging een oplossing van 53

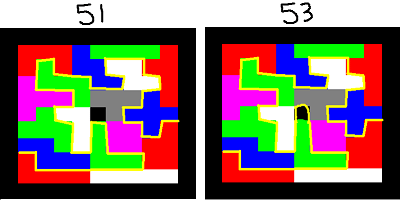
Joe De Vincentis stuurde een pad van 50 stappen.

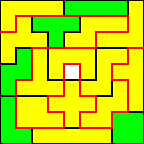
Jens van Pevenage uit 3Latijn van KSO Glorieux Ronse vond 47

Peter Jeuken dacht waarschijnlijk dat hij de configuratie van het veld niet mocht wijzigen.
Hij vond een oplossing met 47 stappen

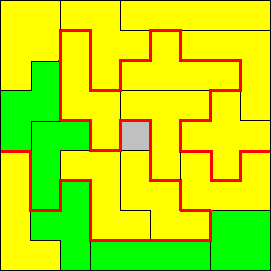
Ted Lakerveld dacht waarschijnlijk ook dat hij de ligging van de polyomino's op het veld niet mocht raken.
Hij vergat ook de voorwaarde "Bovendien, als je het bord langs zo'n pad zou doorzagen valt het in twee stukken uiteen."

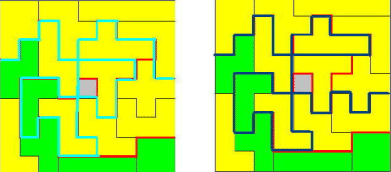
We zijn echter blij dat hij weer meedoet en willen wel zijn lovende woorden belonen.
"Het is je weer gelukt: dank zij je e-mailtje heb je me weer aan het puzzelen gekregen! Ik bewonder je vermogen om mensen, zoals ik bijv., te blijven stimuleren. Het zal voor je studenten een genoegen zijn om van jou les te krijgen. Overigens, mijn inzending zal wel te laat zijn, maar het bewijst dat ik inderdaad gepuzzeld heb."
Bij vaststelling van fouten of onvolledigheid, mail naar: