Many thanks to Bob Henderson (USA) for entering this problem.
Start with a set of pentominoes :
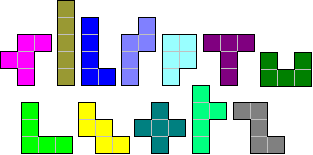
Look for a shape containing all pentominoes once, where every pentomino must border at least one other. In our example there is a hole, of which the outline has a total length of 74 units (the red line).
Try to find a solution with a maximal outline.
When the outlines form two solutions have the same length, the one with the smallest area wins.

For solving the problem Exel can be used. We have a file containing the pentominoes.