Helmut Postl mailde ons een bewijs dat 78 het maximum is:"The first thing we notice is that the perimeter must always be even. This is easy to see. When taking a round trip, then you have to go as many steps down as you go up. So they add together to an even number. Similarly, you go as many steps to the right as to the left, thus again making an even number of steps. The sum of those is again even.
Next, we note the following
Lemma: A pattern that consists of n unit squares can have a perimeter of at most 2n+2.
Proof by induction:
n=1: Just one square with the perimeter 4.
Now assume that the Lemma holds for all patterns with less than n squares.
Divide the n-pattern in two pieces. They have k and n-k squares. So they can have together at most perimeter 2k+2 + 2(n-k)+2 = 2n+4. When gluing the two pieces together, one loses at least 2 units of the perimeter, that gives at most 2n+2.
Now consider the pattern built by the 12 pentominoes. 11 pentos contribute
12 units to the overall perimeter, and the P-pento contributes 10. This makes 142 in total. Let k pentos build the outer ring, then there must be at least 12 gluings where each of those eliminates at least 2 units of the perimeter. Furthermore, each of the remaining 12-k pentos eliminates at least
2 units when being glued to the ring. Therefore the overall perimeter is at most 142-12*2 = 118. This is the sum of the outer and the inner perimeter.
Now assume the inner perimeter be greater than 78, i.e. it is at least 80.
Then there is at most 118-80 = 38 left for the outer perimeter of the ring.
The biggest area with perimeter 38 is a 9x10-rectangle with area 90. Since 60 squares are covered by the 12 pentos, there are at most 90-60 = 30 squares left for the inner hole. But from the lemma above, it follows that this hole can have a perimeter of at most 2*30+2 = 62. This contradicts the assumption of the perimeter to be at least 80.
Meanwhile I succeeded too in finding a 78-solution. It is not easy at all."

Aad van de Wetering:"Het is me gelukt! Het lijkt wel wat op de ‘narrow passage’ maar dan met hier en daar wat extra nisjes."
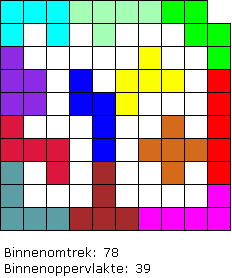
Aad stuurde nog een oplossing:
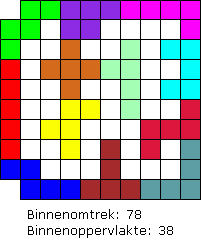
"Deze oplossing voldoet: elke pentomino heeft minstens één zijdecontact, de opening heeft één puntcontact. Dat laatste heb je niet verboden."
We zijn niet akkoord: in Vlaanderen noemt men dit twee binnenruimtes en niet één, maar misschien zien Nederlanders dat anders?
En er kwam nog meer:

"Deze oplossing voldoet, immers elke pentomino heeft “steeds telkens minstens een zijde gemeenschappelijk”. Het is daarbij tevens een geheel, want ook een puntcontact is tenslotte een contact…"
Goed geprobeerd maar we zijn er niet mee akkoord: de pentomino's moeten één geheel vormen!
Het idee van de puzzel was van Bob Henderson en hij heeft er nog andere:
"Here are some solutions for three versions of a puzzle that might be a good competition for your Web site. I used a computer program to find the 10 solutions for an inside perimeter of 78 units using the 12 pentominos (I have not tried to solve this puzzle by hand, but I suspect that it would be very difficult). My computer also found many solutions for the 17 tetro/pentominos inside a 15 by 9 rectangle giving the maximum perimeter of 108 units for the interior hole (this should be easier to solve by hand if more nearly equal rectangle dimensions are allowed). It is also possible to place a double set of 24 pentominos inside a rectangle of 15 by 14 units to give the maximum possible hole perimeter of 178. This was too difficult for my program, but it makes a challanging puzzle to solve by hand!"

Ook Daan Juttmann wist dat 78 maximaal was:
"Ik was er met wat rekenwerk al achter gekomen dat 78 het maximum was."
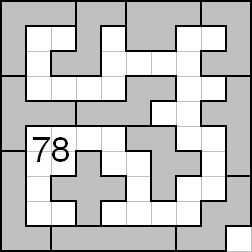
Edo Timmermans mailde het volgende:
"Wat een leuke wedstrijd! Ga ik zeker een oplossing voor insturen. Of hij moeilijk is? Om een goede oplossing te vinden zal niet zo erg moeilijk zijn, om een optimale oplossing te vinden echter wel!"
Hij hield woord!
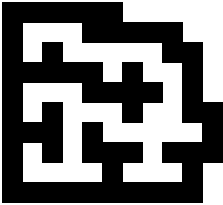
Giacomo Pignatti mailde:"Je suis un ami de Gabriele Carelli, c'est la première fois que je participe à un de tes concours.
Voici une possible solution avec un périmètre interne de 76 et un espace intérieur de 37."
Gabriele bevestigde dit: "As you can immagine I and my wife Silvia are very happy in our new life. But we are also very busy with a lot of thing to do and so I have not much time for puzzles. I know my collegue Giacomo started to think about the competition, he was very intrigued when he saw me playing with pentominoes and so I gave him your web address."
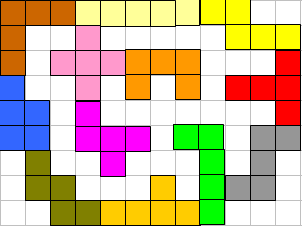
"J'ai une nouvelle solution."
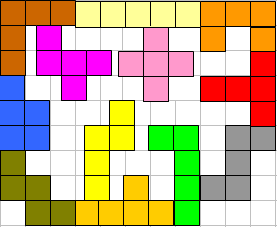
Wat zijn die Italianen toch lepe mannen. (Nog erger dan de Nederlanders!) Als we tellen komen we op 78 uit. Gelukkig kregen we andere oplossingen van 78 want deze oplossing lijkt ons correct volgens onze regels uitgevoerd: er stond nergens dat de pentomino's op het raster moeten liggen. Hij heeft op deze manier wel de kleinste oppervlakte van het gat nl. 33.
Glenn Huysman:"Hierbij de pentomino-oplossing van 76 omtrek"
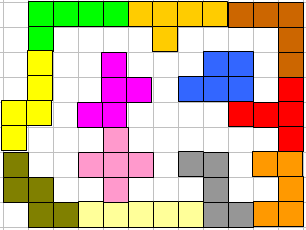
Han van der Pluijm:"De vorm die ik heb gevonden bestaat uit 1 geheel met in de vorm 1 gat met een omtrek van 76 eenheden en 41 vakjes als oppervlakte."
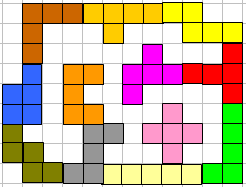
"Sneller dan ik zelf had verwacht vond ik een betere oplossing voor de prijsvraag dan dat ik eerder heb ingestuurd. Ik ben dan ook wel wat uurtjes bezig geweest om deze - naar mijn idee perfecte vorm - te vinden. Mijn vorm bestaat uit 1 geheel met hierin een gat met een oppervlakte van 38. De omtrek van dit gat is 78, net zoals het record tot nog toe. Ik denk dat dit de maximale omtrek is van het gat dat gevormd kan worden met 1 pentominoset, maar of de oppervlakte nog kleiner kan weet ik niet...
Ben erg benieuwd of iemand er in geslaagd is deze kleiner te krijgen!"
Er bestaan natuurlijk slimme Italianen!
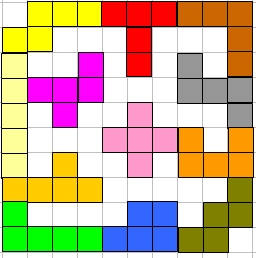
Maaike Kock:"Ik heb een omtrek 74 met een oppervlakte van 42 , maar als Aad al 76 heeft, heeft het toch geen zin dat ik het instuur zeker?"
We zijn echter blij met elke inzending.
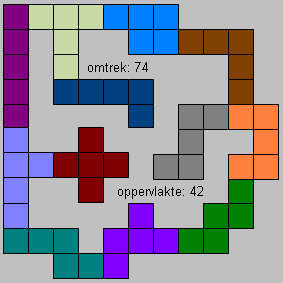
Miyoshi Nagai:"Now, using the pieces of YOUR GIFT, I am trying to solve the problem of your new competition.
Am I in a start line?"

Met 76 omtrek en 39 oppervlakte zat hij zeer goed in de startlijn maar hij haalde de sprint niet!
Peter Jeuken:"De opgave heb ik opgelost met de pentomino's die ik van jullie kreeg. Mijn rode lijn heeft een lengte van 76. Weliswaar geen spectaculaire verbetering van de 74 uit het voorbeeld, maar meedoen vind ik op zichzelf al leuk. De binnenruimte heeft een oppervlakte van 43."

"De oplossing voor de wedstrijd die ik onlangs stuurde is verbeterd. De lengte van de binnenkant is nog steeds 76. De ingesloten oppervlakte is verkleind van 43 naar 39 "

"Driemaal is scheepsrecht zeggen ze wel eens.
Een paar dagen geleden stuurde ik mijn tweede (en betere oplossing) voor de wedstrijd. Maar echt tevreden was ik niet. Daarom heb ik ijverig verder gezocht. Vandaag lag er ineens opnieuw een betere oplossing op tafel. Met een oppervlakte van de binnenruimte van 37 (Het is een foto van de 'Belgische set'die ik met 'paint' heb nabewerkt.)
Het lijkt wel of er een onzichtbare grens bij 76 lijnstukjes ligt. Daarom ben ik benieuwd of dat het inderdaad het maximum is. Wel weet ik dat een oplossing met 77 lijnstukjes niet kan. Alleen even aantallen zijn mogelijk omdat lijnstukjes immers altijd in paren (tegenover elkaar) voorkomen. Dus of iemand 78 vindt? Ik ben buitengewoon benieuwd.
En sinds kort (dominopuzzel van Peter Hendriks) realiseer ik mij (dank zij jullie site) dat dominostenen tot dezelfde familie behoren als de pentomino's."
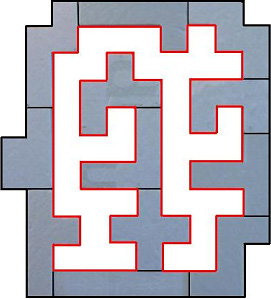
Jeroen De Vos: "Ik hoop dat de deadline van de huidige pentominowedstrijd nog niet is verstreken, want ik wil een oplossing inzenden. Mijn resultaat heeft een binnenomtrek van 76, en een binnenoppervlakte van 37 vakjes (zoals aangeduid)".
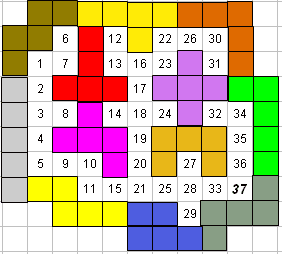
Thomas Termonia:"Ik heb gezocht naar de oplossing van de pentomino-wedstrijd en ben tot 76 gekomen"
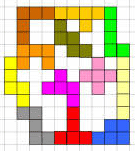
Had Thomas de voorwaarde 'Zorg ervoor dat er één binnenruimte ontstaat' niet goed gelezen of was hij bij Aad in de leer geweest?
