Symmetrie van 1 naar 12 en terug

Met heel veel dank aan Pieter Torbijn
voor de opgave.

Je beschikt over een pentominoset.

Nummer de 12 pentomino's van 1 tot 12
Vorm met deze genummerde pentomino's als volgt 2 series van elk 12 figuren die minstens één symmetrie-as bezitten.
De figuren moeten zonder gaten zijn.
Serie 1: pentomino 1; pentomino's 1+2; ... pentomino's 1+2+...+12
Serie 2:pentomino 12;pentomino's 12+11;...pentomino's 12+...+2+1
We verduidelijken het volgende voorbeeld.
Het is echter geen juiste oplossing omdat alle figuren zonder gaten moeten zijn!



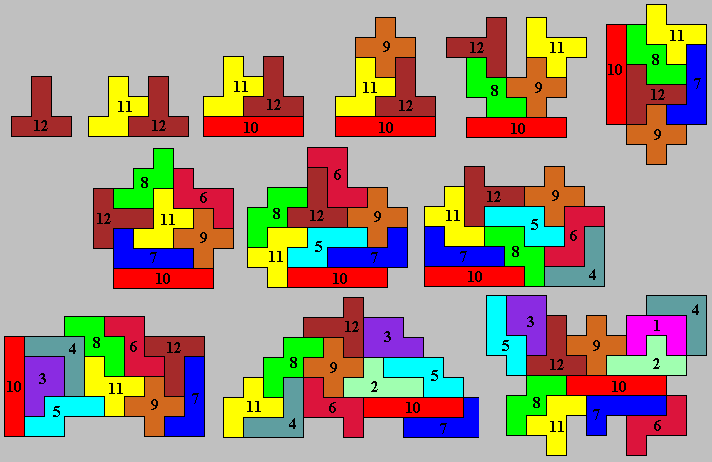
De laatste figuur kregen we als symmetrische vlinder toegestuurd van Reinhard Grafl uit Oostenrijk.
We begonnen met de U-pento en eindigden bij de T-pento. Hoe meer verschillende voorbeelden je toestuurt, hoe groter de kans dat je onze winnaar wordt.
Wil je nog een extra uitdaging?
Zoek naar een oplossing met een maximale of een minimale totale omtrek voor de 23 symmetrische vormen. (De vorm met de 12 pentomino's telt maar éénmaal)