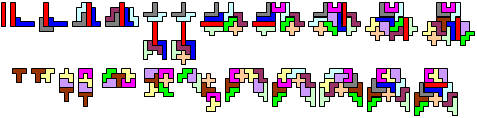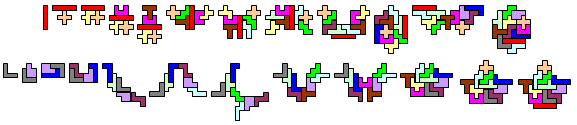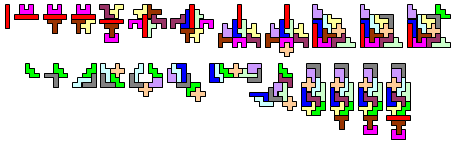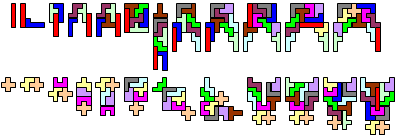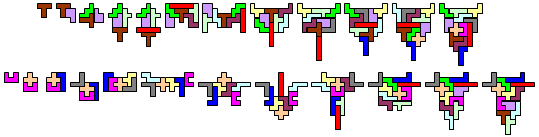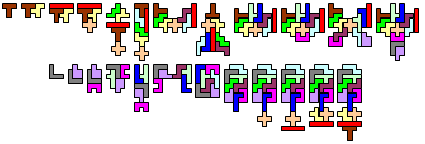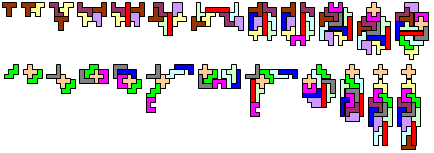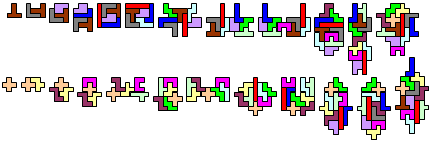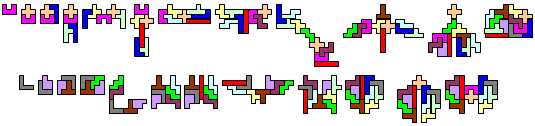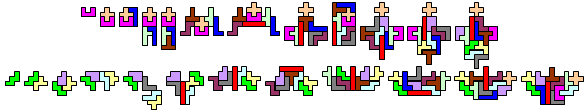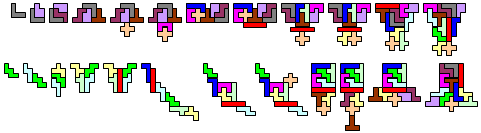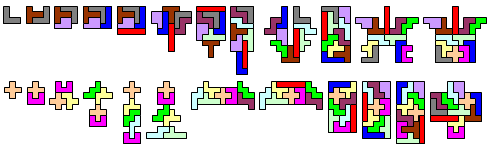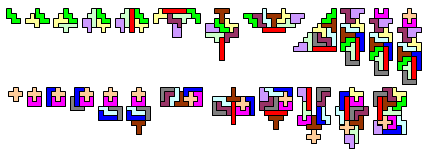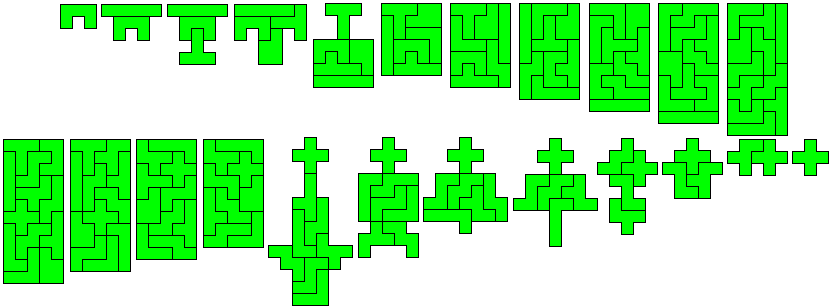Records Wedstrijd 35
De grootste luiaard, maar misschien wel de slimste is Edo Timmermans.
Hij mailde:"Net heb ik naar de opgave gekeken. Helaas is het voor de opgave mogelijk een heel eenvoudig antwoord te geven: hernummer 1-2-3-4 tot 4-3-2-1; de nieuwe 1 is symmetrisch, met de nieuwe 1 en 2 kun je heel makkelijk een symmetrische vorm maken, met de nieuwe 1,2 en 3 is dat ook niet moeilijk, zie bijlage. Tenslotte hoef je alleen maar voor het 9e, 10e en 11e geval in de 2e serie symmetrische plaatjes te vinden met de juiste nummering, die stuur ik morgen wel op. De rest blijft het zelfde als in het voorbeeld."

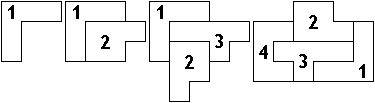
"In plaats van zoveel mogelijk oplossingen te vragen lijkt het me geschikter om te vragen naar oplossingen waarbij de totale omtrek van alle figuren maximaal is. Dat is het moeilijkste om te vinden, tevens krijg je dan leuke vormen."

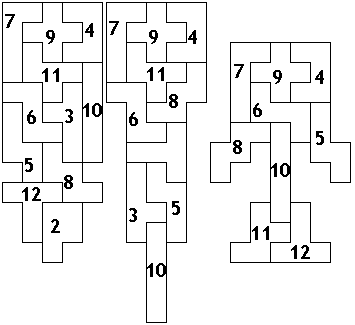
Dat lui zijn moeten we echter herzien want er kwam nog een oplossing:
"Het is natuurlijk altijd mogelijk om bij de wedstrijd de echte pento-fans uit te nodigen oplossingen met minimale of maximale totaal-omtrek te zoeken. De bijlage bevat mijn oplossing met maximale totaal-omtrek."


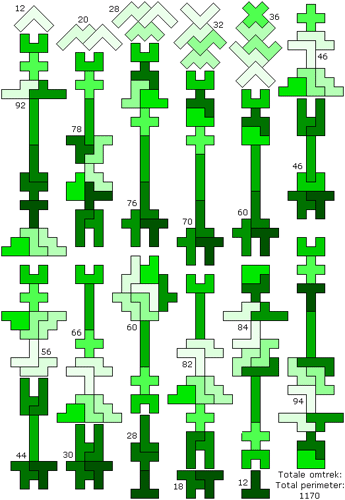
Helmut Postl brak dit record.
"My minimal perimeter sum is 528. The sequence of pentos is V, N, Z, L, I, U, R, X, T, Y, P, W.
My maximal perimeter sum is 1238. The sequence of pentos is V, N, R, Z, L, I, T, Y, U, X, P, W."

Bob Henderson wou ook dit laatste record breken en slaagde erin.Wat is hij leep!
 "I hope that you like the attached solution for the symmetric series pentomino puzzle. The 23 shapes have a total perimeter of 524 units. If you are looking for the axis of symmetry for the Z pentomino, it goes through the center at a 90 degree angle to the pentomino plane! Congratulations to Helmut on his maximum perimeter solution. I don't think that I will find enough time to look for a larger perimeter."

Bob Henderson:" I did not try very hard to minimize the combined perimeter of the 23 shapes, so my total of 566 may not be much better than average. Because of the rule that every shape must be symmetric, I thought that it would be more interesting to try to find as many additional symmetries as possible. Of the 8 rotations and reflections for a given shape, I counted each that matches the original shape as a measure of symmetry: a non-symmetric shape has only one that matches, a shape with one axis of symmetry has 2 that match (the original shape and its reflection), a shape with both vertical and horizontal axes of symmetry has 4 that match, and a shape that also looks the same after a 90° rotation has all 8 of its rotations and reflections matching the original shape. You might prefer some other way to count the symmetries if you decide to compare the amounts of symmetry for different solutions."
"Here is a small improvement from 566 to 560 perimeter"
"I found another small improvement to a net perimeter of 556 (292 + 296 - 32) for 23 symmetrical shapes."
Peter Esser:"It was a nice possibility to combine some manual solving with some computer solving for the rectangles.
Thank you very much."
Peter Jeuken:"Hartelijk dank voor de pentomino puzzel van Pieter Torbijn die mij vele uren puzzelplezier heeft bezorgd.
Voor mezelf heb ik nog een extra voorwaarde toegevoegd. Alle samenstellingen van 1 t/m 12 en van 12 t/m 1 hebben precies één as van symmetrie en wel een diagonale. Dat betekent dat de uiteinden van de serie worden gevormd door de V en de W. Bij het kiezen van de tussenliggende pentomino nummers ben ik diverse malen vastgelopen maar uiteindelijk ben ik er toch uit gekomen.
Ik heb dankbaar gebruik gemaakt van de pentomino set die jullie me vorig jaar gestuurd hebben. Bovendien had ik ondersteuning van een door mij geschreven computerprogramma."
Christian Miaskiewicz:"Votre concours est très intéressant, je me suis bien amusé à rechercher une solution.
Vive les pentaminos et encore bravo pour votre formidable site."
Met zo'n commentaar moeten we hem wel winnaar maken ;-).
 En er kwam nog:"Les pentaminos, une fois qu'on a mis le nez dedans c'est difficile de s'en sortir. Etant enseignant amené à remplacer dans de nombreuses écoles primaires et maternelles je ne manque jamais une occasion de faire découvrir les pentaminos à mes élèves et de parler de votre site."
"Je m'amuse comme un fou, voici une nouvelle solution pour votre concours."
"Je vous envoie ma solution n° 14. C'est vraiment passionant cette recherche."
"Voici ma solution n° 16. Je crois que ça va être difficile pour moi d'en trouver d'autres."
Niets was minder waar; we kregen van Christian 57 oplossingen.
"Chez moi il pleut des cordes ce matin alors chercher des solutions me passe le temps. Et depuis des années je suis épaté par tout ce qu'on peut faire avec ces 12 pièces. Ici les gens connaissent tous les tangrams mais je trouve que les pentaminos sont bien plus riches. Alors comme je remplace dans différentes écoles j'ai l'occasion de faire découvrir les pentaminos à de nombreux élèves qui sont toujours enthousiasmés. Et peut-être qu'un jour les pentaminos seront aussi célèbres que les tangrams. En tout cas votre site est un incontournable pour ce jeu."
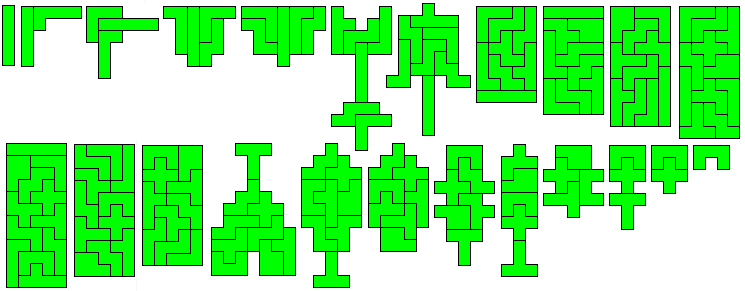
Hier volgen Christians oplossingen voor een deel. (Van I naar U en van U naar X was er niet bij)
De volledige lijst kan je vinden door op zijn naam te klikken.

I naar T

I naar V

I naar W

I naar X

T naar U

T naar V

T naar W

T naar X

U naar V

U naar W

V naar W

V naar X

W naar X

Een eerste reactie kregen we van Stefano Popovski: "U to X looks possible for me. Can't tell right in the moment as I'm at work. Will give it a try. The other could be more difficult, the U makes usualy the biggest problems with symmetric configurations when comes at end. The U fits well in only 1 diagonal group with another pentomino - the L and on straight symmetrical groups fit's only on odd sides, this way is too restrictive too keep it for the end. Will see, for this problem I have appeal.
Has somebody by program or mathematical means a prove, that symmetric chains from any to any are possible? I know however, that it's very difficult to prove something as a theorem in the combinatorics."
Peter Esser stuurde ons echter voor beide een oplossing:" I tried to make one of the missing sequences of symmetric shapes as described in competion no 35. The U > I sequence is attached. Perhaps I'll try the other sequence, too."

"Just the last sequence X to U. Nice problem indeed."


In de lijst vind je de namen van degenen die ons een oplossing stuurden.
Je kan de inzending bekijken door op de naam te klikken.