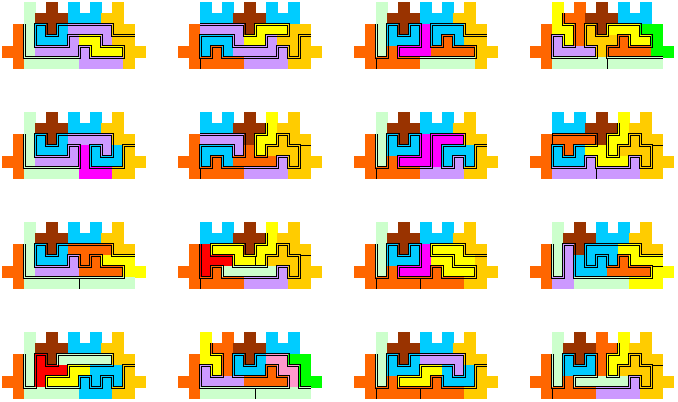Records Wedstrijd 38

Aad van de Wetering was zoals gewoonlijk de eerste om een oplossing in te zenden. Hij beschikt over heel wat mogelijkheden om een oplossing te zoeken:"Ik heb een programmaatje geschreven, erg veel werk is dat niet. Als ik dat goed gedaan heb zijn er twee oplossingen met padlengte 33, namelijk nummer 51 en 78 van FlatPoly2 (symmetrische oplossingen uitsluiten, totaal aantal oplossingen 112)."
Er zijn er echter drie.


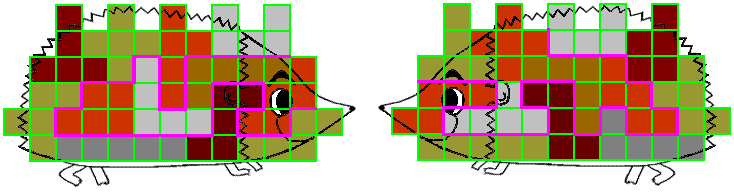
We hebben echter nog heel slimme vrienden.
Peter Jeuken mailde:"Puzzelen is verslavend. Dat geldt zeker ook voor puzzelen met pentomino's.
Mijn computerprogramma heeft 112 verschillende egel-oplossingen gevonden. Met langste knips van 19 eenheden tot 33 eenheden.
Drie knips van 33 eenheden één knip van 19 eenheden staan in de bijlagen. Interessant dat alle oplossingen beginnen met 'T'en 'X' "





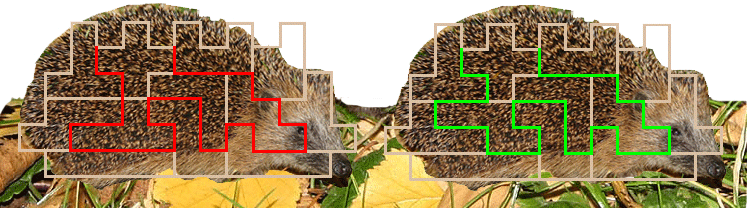
Helmut Postl zond ons ook een variatie waarbij de egel verdeeld is in 2 gelijke delen d.w.z. dat elk deel bestaat uit 6 pentomino's.
De maximale padlengte is dan 31

Bob Henderson en Helmut Postl zonden 4 oplossingen in van een knip van 33.
De knip is verschillend maar er zijn 2 dezelfde pentomino-egels bij.
We willen dat rekenen als 3,5 oplossingen;-)

In de lijst vind je de namen van degenen die ons een oplossing stuurden.
Je kan de inzending bekijken door op de naam te klikken ofwel staat ze hierboven.