Onze inspiratie haalden we dit keer bij Peter Hendriks puzzel 206.
Helmut Postl maakte voor ons een analoog probleem.
Aad van de Wetering controleerde het.
Bedankt allemaal.
Hieronder vind je één van de twee rechthoeken van 3x20 die we kunnen maken met een pentominoset.
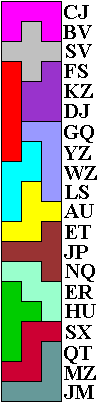 |
In elk van de vijf vakjes van een
pentomino komt één van de cijfers 1, 3, 5, 7 of 9 te staan. In elke pentomino zijn de vijf cijfers alle verschillend. Er ontstaan zo onder elkaar 20 getallen van drie cijfers. Ieder van die getallen kan in twee priemfactoren worden ontbonden. De twee letters in dezelfde rij rechts geven die factoren aan. Gelijke letters zijn gelijke factoren, en omgekeerd. Hoe komen de cijfers in de pentomino's te staan? De oplossing is enig. |
Om de puzzel op
te lossen maakte Toby dit applet
http://www.gottfriedville.net/puzzles/pentprime/index.html