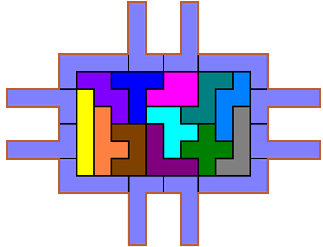
Van sommige deelnemers kregen we een bewijs dat 88 de maximale omtrek was.
Aad van de Wetering mailde:"Elke pentomino van de omsluitende figuur heeft contact met de rand van de binnenfiguur én heeft contact met twee buren. Een pentomino heeft een maximale omtrek van 12, in totaal 12 x 12 = 144. Daar gaan er voor elke pentomino minstens 2 af voor contact met zijn buren, en verder de omtrek van de binnenfiguur. De kleinst mogelijke omtrek van een set pentomino’s is 32. De maximale omtrek van de complete figuur is dus 144 – 2 x 12 – 32 = 88, en dat is het dubbele van het wedstrijdnummer."
Dit zijn onze deelnemers :
(voor hun oplossing te zien, klik op hun naam)
|
Naam |
Land |
| Wouter Boogert | Nederland |
| Marco en Lorenzo Carelli | Italië |
| Joe DeVincentis | USA |
| Bob Henderson | USA |
| Peter Jeuken | Nederland |
| USA | |
| Polen | |
| Oostenrijk | |
| Edo Timmermans | Nederland |
| Aad van de Wetering | Nederland |
| R. Wainwright | USA |
Leuk idee voor een volgende wedstrijd.
Bij vaststelling van fouten of onvolledigheid, mail naar:
