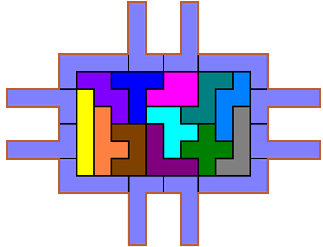
Van sommige deelnemers kregen we een bewijs dat 88 de maximale omtrek was.
Helmut Postl mailde:"Proof: Each pentomino has a perimeter of 12, except the P which has 10. So the maximal perimeter of the 12 red pieces is 12×12 = 144. Since they are connected to each other by at least twelve times a single side, this means that each piece has 12 – 2 = 10 open sides left. So the constructed red ring has at most 120 open sides. This is the sum of the inner and the outer perimeter. So in order to maximize the outer perimeter, we have to minimize the inner perimeter. In other words, we have to find a shape of area 60 which has minimal perimeter. It is easy to see that this minimum is 32, and it can be achieved in several ways, for example a 6×10-rectangle. This means that the outer perimeter is at most 120 – 32 = 88."
Dit zijn onze deelnemers :
(voor hun oplossing te zien, klik op hun naam)
|
Naam |
Land |
| Wouter Boogert | Nederland |
| Marco en Lorenzo Carelli | Italië |
| Joe DeVincentis | USA |
| Bob Henderson | USA |
| Peter Jeuken | Nederland |
| USA | |
| Polen | |
| Oostenrijk | |
| Edo Timmermans | Nederland |
| Aad van de Wetering | Nederland |
| R. Wainwright | USA |
Leuk idee voor een volgende wedstrijd.
Bij vaststelling van fouten of onvolledigheid, mail naar:
