Inzending van Peter Jeuken

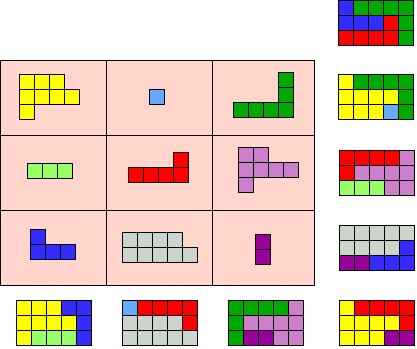
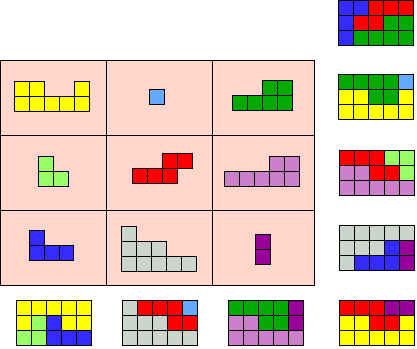
Van Peter Jeuken kregen we de volgende mail:"Bij de oplossing van wedstrijd 47 heb ik mezelf nog een extra beperking opgelegd, namelijk dat het doel een 3x5 rechthoek is.
Voor drie pentomino's heb ik een oplossing gevonden, de I, de P en de V. Ik ben benieuwd of er puzzelaars zijn die ook met andere pentomino's in het midden een rechthoek kunnen maken."

Met deze voorwaarde was dit juist vraag 4 van de prijsvraag van het tijdschrift Pythagoras.
Er zijn hiervoor 1411 verschillende oplossingen. Helmut Postl zocht dit voor ons uit.
Als je alle oplossingen wil vraag je het maar: o.d.m@fulladsl.be
Voor de wedstrijd van Pythagoras geldt echter: twee oplossingen zijn verschillend als ten minste twee van de figuren verschillen.
Er blijven dan 205  oplossingen die we in 2 PP geplaatst hebben en die je kan downloaden
http://users.fulladsl.be/~spb33365/Vraag4goed1.ppt
http://users.fulladsl.be/~spb33365/Vraag4goed2.pps

 

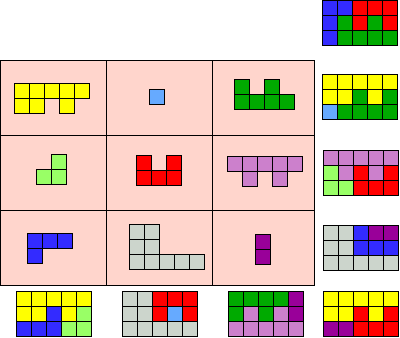
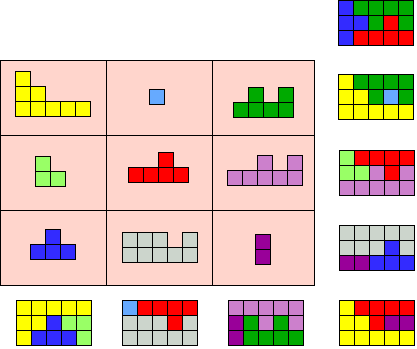
We denken dat er nog vier andere mogelijkheden zijn : L, N, U en Y