Vertrek van een set pentomino's en werk in het vlak.


Verdeel de set in 4 groepen van 3 pentomino's.
Maak met de 3 pentomino's telkens een vorm die een symmetrie-as heeft.
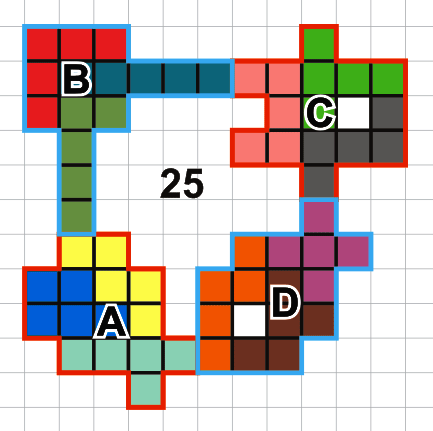
Deze 4 symmetrische vormen (A,B,C en D in het voorbeeld) maken een omheining waarbij je probeert van zoveel mogelijk vierkantjes in te sluiten.
De pentomino's liggen op het raster en moeten telkens minstens een zijde gemeenschappelijk hebben.
 In het onderstaande voorbeeld zijn 25 vierkantjes ingesloten.

Misschien kan je onder de knop symmetrie (in het frame) hulp vinden.