Problème de Kate Jones.
Remplissez le chiffre 50 à l’aide des 12 pentominos, 5 tétrominos, 2 trominos, du domino et du monomino.
Les tétrominos, trominos, le domino et le monomino ne peuvent pas se toucher, même pas par les angles.
Kate aimerait aussi savoir si vous l’avez résolu vous-même ou si vous vous êtes fait aider par l’ordinateur.
Pour vous aider à le résoudre vous-même, nous avons réalisé ce fichier exel et aussi un fichier geogebra.
Au cas où ce ne serait pas clair, adressez-vous à
o.d.m@fulladsl.be

FlatPoly a calculé qu’il y a plusieurs solutions possibles.
Vous pouvez télécharger Flatpoly ici:
http://home.wxs.nl/~avdw3b/aad.html

C’est aussi Kate Jones qui a eu l’idée de notre concours 34

Problème de Bob Harris
(A) Choisissez un pentomino, faites-en 13 copies en jaune; choisissez un tétromino et faites-en 4 copies en noir.
(B) Placez les pièces de façon à remplir un carré de 7x7. Les pièces jaunes sont "positives" et valent +1; les pièces noires sont "négatives" et valent -1.  Les pièces noires doivent se superposer aux jaunes.
Au lieu de prendre 13 copies du même pentomino, il est aussi possible d’utiliser un set de pentominos et un pentomino supplémentaire ainsi qu’un set de tétrominos en enlevant un tétromino au choix.

L’idée vient de là: http://www.bumblebeagle.org/polycubes/7andF.solution.gif
La question était: réalisez un cube de 4x4x4 à l’aide de copies d’un heptacube et d’un pentacube. De combien de copies de chaque sorte a-t-on besoin? Notre solution: 7a + 5b = 64 . Le a et le b sont des nombres entiers naturels. Les solutions sont: a=2 et b=10 ou encore a=7 et b=3.

Pour cette consigne-ci, c’est la surface qui pose problème: remplir un carré de 7x7 à l’aide de pentominos et de tétrominos.  Notre solution: 5a+4b = 49 et le a comme le b sont des nombres naturels. Les solutions sont (9,1), (5,6), (1,11).  Il y a davantage de solutions si a et b peuvent être des nombres entiers. Par exemple (a,b) = (13,-4) donc 13 pentominos et 4 tétrominos négatifs.
Dans notre exemple, nous avons choisi le pentomino en L et le tétromino en L.
Passez la souris sur le dessin.

Pouvez-vous le faire avec d’autres pentominos ?

Problème de Martin Watson
 Martin Watson nous a donné l’idée de notre concours 21.
Placez les 12 pentominos dans un carré de 12x12 sans qu’ils se touchent, pas même par les angles.
Comptez le nombre d’unités de pentominos touchant les côtés du carré.
Essayez de le faire avec un maximum et avec un minimum d’unités.
  Dans cet exemple il y en a 32.


Problème de Peter Jeuken
Peter a inventé ce puzzle pentomino spécialement pour nous.
12 sets de 12 pentominos et 12 sets de 5 tétrominos composent un carré de 32x32 dont les 4 coins (carrés de 4x4) manquent.
Pour l’agrandir, cliquez sur le gif.
 
Découpez la figure en 12 morceaux de manière à ce que chaque pièce comporte précisément 12 pentominos différents et 5 tétrominos différents.
On ne peut découper qu’en suivant les motifs sur la grille. Les pentominos et tétrominos doivent rester entiers.
S’il y a plus d’une solution, la gagnante sera celle dont les 12 pièces totalisent le plus petit pourtour.

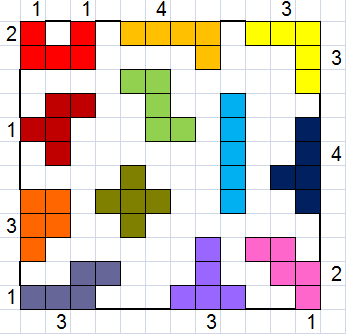
Problème de Aad Thoen : les îles de Pentominos
Disposez tous les pentominos comme des îlots dans la mer, la mer doit être la plus petite possible.

Dans notre exemple, la mer compte 122 unités.

Notre consigne pot-pourri 11 est une variante de celle-ci; la mer devait être un rectangle.

Dans une autre consigne, nous permettons que les pentominos soient des presqu’îles. La forme de la mer doit être un carré, c’est ce que nous avons fait dans la consigne pot-pourri 12

Problème de Aad van de Wetering
Nous remercions Aad van de Wetering grâce à qui notre site pentomino est ce qu’il est.
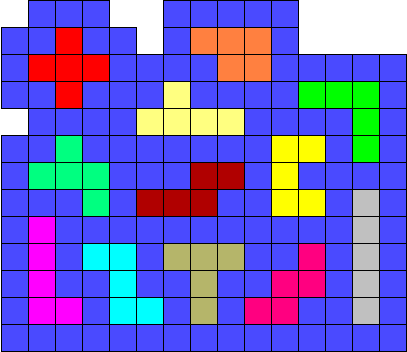
1 + 1 = 3
Cette consigne vient de notre ami Pieter Torbijn qui est décédé depuis et à qui nous dédicaçons tout ce concours.
Encadrez un set de pentominos à l’aide de deux autres. Le carré total doit être le plus petit possible.


Dans notre exemple, le carré fait 16 x 14
On peut voir une solution de Michael Keller ici :
http://www.solitairelaboratory.com/pentmino.html.
  Il s’agit d’un carré de 18 x 13. Mais on peut faire encore beaucoup mieux.
 
Xudoku-Pento-Produit
A notre demande, parce que nous savons que nous avons ici des fans de sudoku, Aad van de Wetering a réalisé cette belle consigne.
Martin Friedeman: "Wat een geweldige puzzelmaker is Aad toch!" (quel fantastique faiseur de puzzles!)
Matthijs Coster:" Ik doe met één van jouw prijsvragen mee. Op de NWD leerde ik dat het ging om een calcudoku, maar een lastige, en vooral leuke. Nergens hoefde er te worden gegokt" (Je participe à un de tes concours. J’ai appris qu’il s’agissait d’un ‘calcudoku’, difficile mais surtout amusant, ce n’est jamais une question de hasard)

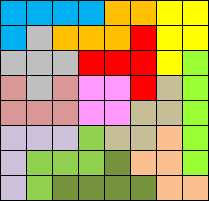
Placez les chiffres de 1 à 8 dans chaque rangée, chaque colonne et dans les deux diagonales.
Vous recevez le produit des nombres de chaque pentomino.

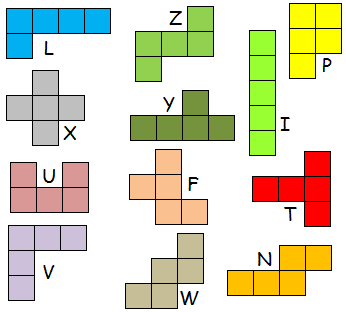
L:420, X:96, U:1080, V:11760, Z:576, Y:336, F:1440, W:84, P:720, I:1120, T:384 , N:1680
Besoin d’aide? Ecrivez à o.d.m@fulladsl.be

'50. Fifty-Fifty' Problème de Edo Timmermans
Comme Edo est un de nos fans les plus créatifs (voir le concours de cartes postales pentomino et
L’île du comte Penteviticole) nous lui avons demandé de réaliser une consigne.
Il l’a appelée: "50. Fifty-Fifty"
Son concours se compose de 2 parties.
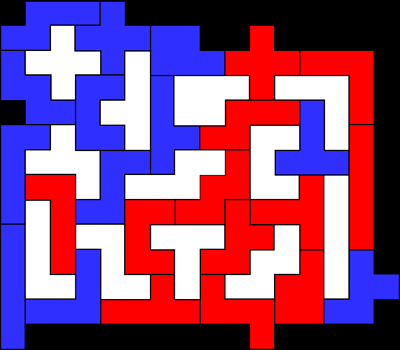
Prenez un carré rouge de 10x10 avec à l’intérieur en diagonale un carré vert qui recouvre 50% de la surface du carré rouge de 10x10.
Placez les pentominos à l’intérieur du carré rouge de 10x10 de manière à ce qu’ils soient tous en partie rouges et en partie verts.


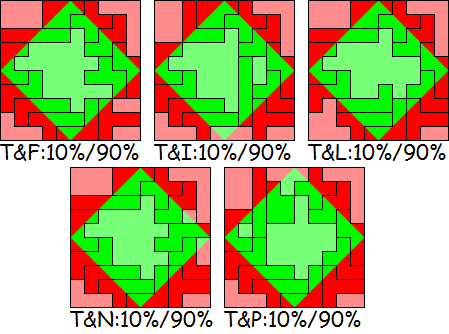
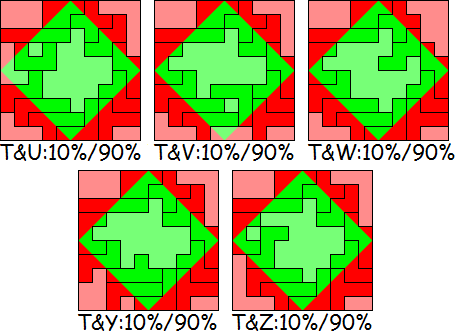
Dans la première partie du concours, le but est de trouver des solutions dans lesquelles 10 pentominos sont rouges à 50% et verts à 50%. De plus, tous les pentominos réunis doivent être à 50% rouges et à 50% verts. On peut voir aux exemples que ce n’est pas si difficile, quand les 2 autres pentominos peuvent être rouges à 10% ou verts à 10%. Voilà pourquoi nous demandons qu’ils le soient à au moins 20%, et bien entendu, au plus on se rapproche des 50%, au mieux c’est.

Dans la deuxième partie du concours, il faut trouver des solutions symétriques. Il ne s’agit plus d’avoir 10 pentominos à moitié rouges et à moitié verts, chacun doit être en partie rouge et en partie vert et tous ensemble ils doivent être rouges à 50% et verts à 50%.

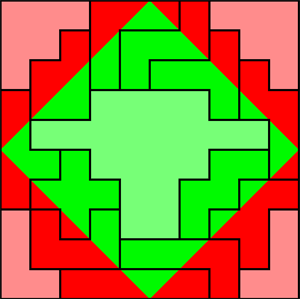
 Cet exemple n’est pas une bonne solution parce que le pentomino W est complètement vert.
Nous invitons les programmeurs à trouver des solutions symétriques dans lesquelles 50% des pentominos sont rouges à 50% et verts à 50%.

Pentorigami-Problème de Bob Henderson
Confectionnez un set de pentominos en papier de couleur.
Nous vous avons préparé des pages avec 6 fois chaque pentomino pour que vous puissiez en faire des photocopies sur papier couleur. Vous obtenez ainsi plusieurs sets de pentominos.
F I L N P T U V W X Y Z
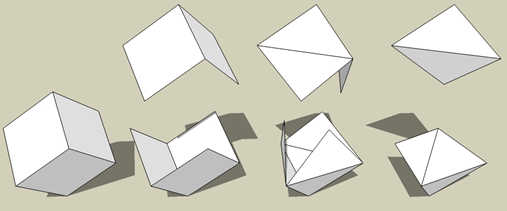
Coupez également une des lignes centrales du pentomino P.
Il y a 8 pentominos qui permettent de fabriquer une petite boîte ouverte: F,L,N,T,W,X,Y en Z
Réunissez 6 de ces petites boîtes : on dirait que 6 cubes sont collés aux parois d’un 7^e cube central invisible. 

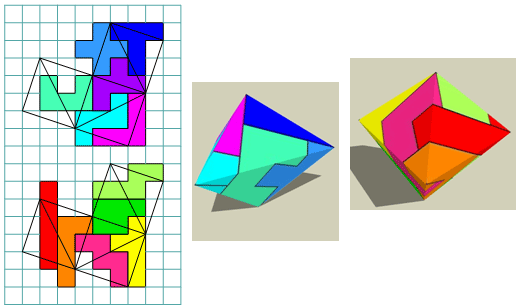
Prenez les pentominos I,P,U et V (ceux avec lesquels il est impossible de confectionner une petite boîte ouverte) ainsi que 2 autres pentominos. Essayez de réaliser un pliage et de rassembler le tout pour former la même figure que ci-dessus. Tous les pliages sont permis.

3D-Problème de Michael Dowle
Michael recouvre un cube d’un set de pentominos.

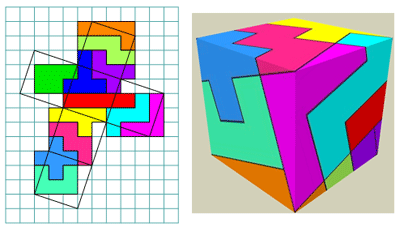
Il y a quelques années que les élèves de 3e de l’école KSO Glorieux recouvrent un cube dans le cadre de leurs cours sur Pythagore.
http://www.pentomino.classy.be/versnijdenopkubus.html
Aad van de Wetering recouvre le cube à l’aide du même pentomino.  
http://home.planet.nl/~avdw3b/kubuspoly.html
C. J. Bouwkamp a écrit un livre en 1998 (qu’il nous a offert) "Tiling the surface of the cube by 12 identical pentominoes"
On trouve d’autres idées de cubes recouverts sur les sites ci-dessous :
http://www.ericharshbarger.org/pentominoes/article_06.html
http://www.tzingaro.com/artelectric/pentominoes06.html
http://home.educities.edu.tw/proteon/note131.htm
http://www.iread.it/lz/pag3_eng.html

Michael recouvre aussi des dipyramides triangulaires

Voilà une chose que nous n’avons vue nulle part ailleurs.
Voici maintenant sa très belle consigne:
Trouvez une façon de placer un set de pentominos pour en recouvrir un cube de manière à pouvoir le diviser en deux moitiés qui sont des dipyramides  triangulaires.  
Il n’est pas permis de changer l’ordre des pentominos.
Le dessin ci-dessous présente le problème.


Pentominos à la ficelle
 Notre inspiration vient d’un livre amusant "Denkwaar" de Jaap Klauwen.
Merci à Aad Thoen qui nous l’a fait parvenir.
Pour vos calculs, vous utiliserez le théorème de Pythagore.
On fait coordonner les angles des pentominos avec des points de la grille. Chaque côté d’une case compte pour 1. Chaque pentomino doit avoir au moins un côté en commun avec un autre.
Nous tendons une ficelle autour des points de la grille contenant les sets de pentominos.
Placez les pentominos de façon à obtenir un pourtour maximal.
 
Dans l’exemple ci-dessus, la ficelle tendue (ligne verte) vaut 71.98 (précision jusqu’à 0,01).
Essayez d’obtenir un maximum.

 
Problème de Alexandre Owen Muniz
Alexandre nous a envoyé un message avec une consigne pour le concours mais nous ne la comprenions pas bien. Helmut Postl nous en a donné une belle explication.
La transformation d’un polyomino veut dire qu’on déplace un carré d’un polyomino pour former un autre polyomino.
Par exemple, d’un tétromino L on peut faire un tétromino T.

Puis transformer à son tour le tétromino T et ainsi de suite. De cette façon, on peut réaliser une chaîne de tétrominos.
Quand chaque tétromino n’apparaît qu’une fois dans la chaîne, et que le premier et le dernier sont identiques, on a réalisé un cycle complet. Dans le cycle, il n’est pas important de savoir quel tétromino a servi de point de départ, puisqu’un cycle n’a ni début ni fin.
Dans l’exemple ci-dessous, chaque carré du tétromino a sa propre couleur pour qu’on voie bien les déplacements:

Ce cycle comporte 5 tétrominos (L,N,Q,T,I) et peut être répété à l’infini.
Remarque: le L final est coloré différemment du L initial mais ça n’a aucune importance.
Dans un cycle, le polyomino final doit avoir exactement la même orientation que le premier, donc se trouver exactement dans le même sens que celui de départ. Dans l’exemple ci-dessus, le déplacement est une permutation identique (vecteur zéro). Entre le début et la fin du cycle, le tétromino est resté à la même place.
Dans l’exemple suivant, le tétromino final s’est déplacé selon le vecteur (2,1):

En poursuivant ce cycle, le tétromino continuera de se déplacer.
La vitesse de ce mouvement est mesurée par le vecteur inhérent au déplacement du polyomino à l’intérieur du cycle.
Dans l’exemple ci-dessus, c’est (2,1).
La vitesse est la somme des valeurs absolues des nombres de coordination, donc 3. Cette façon de mesurer est plus naturelle qu’avec la distance euclidienne
(dans ce cas-ci la racine carrée de 5). Alexandre appelle cela le 'taxicab distance' parce que c’est la distance que prend un taxi pour suivre la route (les lignes de la grille).
La vitesse du cycle dans le premier exemple est zéro.

Problème d'Alexandre
Prenez les 12 pentominos et réalisez un cycle dans lequel la vitesse est maximale.
Vous pouvez aussi le faire avec des hexominos ou avec les pentominos à une face.
 Remarque: ce problème rappelle 'Conway’s Game of Life'
Ces cycles de polyominos ressemblent au mouvement appelé 'glider'

Le vecteur est (1,1)

Appendice
Nous trouvions que 12 consignes pour le 50^e concours, c’était un joli nombre, mais George Sicherman nous a envoyé un puzzle qui convient parfaitement : 'Fifty Puzzle'
Enlevez 2 pentominos d’un set de 12 de sorte qu’avec les 10 qui restent vous ne puissiez plus faire un rectangle d’une surface de '50'
Il n’y a qu’une seule solution.
 

Remarques de Helmut Postl: "You can even omit the '10x5'-condition and ask for any rectangle since the 10x5 is the only possible one.
It would have been a nice '50'-puzzle since it equals the area of the rectangle. And curiously enough, FP are the initials of 'Fifty Puzzle'".