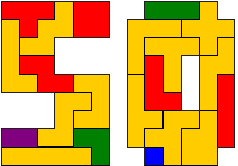
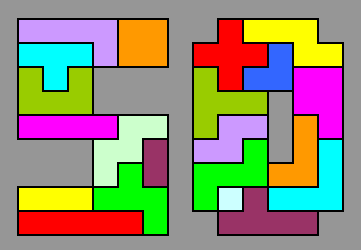By Kadon Enterprises can buy you a chain-pentomino. We put the pentominos in the same way as in the picture. Flat Poly told us that this solution is unique!
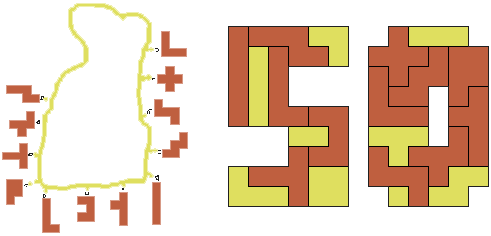
Peter Jeuken (The Netherlands) searched for the maximum number of polyominos 1 to 4 (which are not allowed to touch one another) in the 5 or in the 0. With the aid of the computer, he found a solution with 7 polyominos in the 5 and a solution with 7 polyominos in the 0.
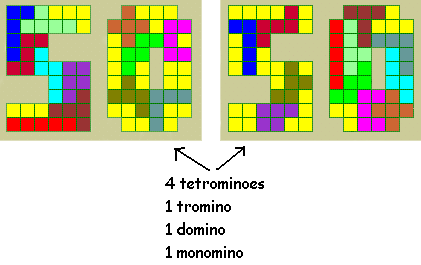
We got this dialogue between two pentomino puzzle solvers also from Peter Jeuken
The two puzzle solvers introduce themselves.
P: My name is Peet. I love solving pentomino puzzles. The only tools I use are paper, pencil and rubber.
J: My name is Jeek. I love writing computer programs in general, and puzzle solving programs in particular. One of the programs I have written is a tool for finding perfect-fit-solutions of objects (such as polyominoes) in a predefined field.
P and J start a dialogue.
P: Hi Jeek. Recently I saw a polyomino puzzle presented by Kate Jones as part of an anniversary contest.
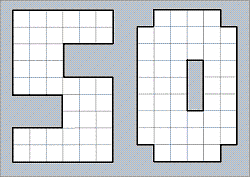
Fit all the polyominoes from 1 through 5 into the grid within the number 50, so that no two of the tetrominoes, trominoes, the domino and monomino touch each other, not even at the corners.
P: I propose that we both solve the puzzle. I do it my way, you do it your way.
J: That is a good idea. Basically it is not too complicated for my computer program. However, the extra restriction that polyominoes 1 through 4 are not allowed to touch each other is not supported. An extension to handle this extra condition is required.
P: I propose we meet again next week. Hopefully you can show a computer solution then. My task is to find a solution by hand.
J. OK. I am going to implement the extension. See you next week.
P and J meet again one week later.
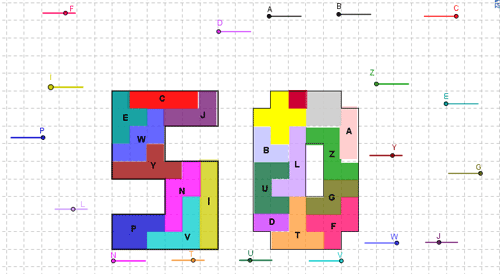
P: This is my solution. Six pentominoes and three tetrominoes in the 5. All other polyominoes in the 0.
J: This is my solution.
The pentominoes are represented by F I L N P T U V W X Y Z
The tetroninoes are represented by i l o t z
The trominoes are represented by 3
The domino is represented by 2
The monomino is represented by 1

As a matter of fact, this is the first solution from a long list.
P: Lets send in these two solutions for the anniversary contest.
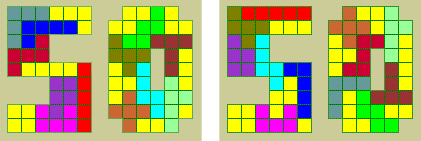
J: Do you think that one might guess which solution is found by a human and which solution is found by a computer?
P: I think so. Your fitting program must operate according to a fixed plan. For instance from left to right and from top to bottom. And probably the pentominoes are fitted in alphabetical order. Note that the solution on the right side starts with F and I which are the first two pentominoes in alphabetical order. So, this is a good candidate for the computer solution.
Dario Uri mailed:"The problem of Kate admits a lot of solutions, I have chosen this because it is the only one that I have found where in the number 5 there are seven pentominoes, in all the other solutions the pentominoes are separated six and six for the two figures 5 and 0."
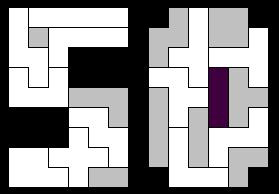
Peter Esser mailed:"Fixing some of the smaller polyominoes at places in the '5' by hand, the computer could finish the whole pattern immediately.The third solution met all conditions."
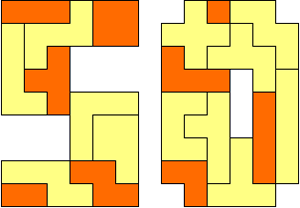
and "I'm sorry to hear that this is the last competition; it was alwas great fun and I appreciate your work very much. Thanks a lot."
The following resolution is of Frank Tinkelenberg.
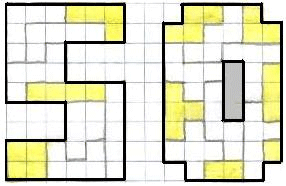
The small pieces are shaded so you can easily see that they do not touch

Helmut Postl mailed: "It was not too difficult to find a solution by hand. The many small pieces provide a lot of varieties."