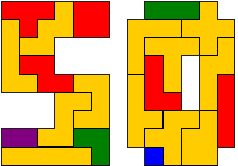
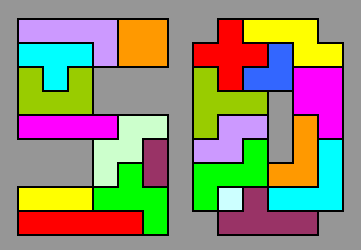Bij Kadon Enterprises kan je een pentomino-ketting kopen. We legden de pentomino's op dezelfde manier zoals in de afbeelding.
FlatPoly vertelde ons dat deze oplossing uniek is !
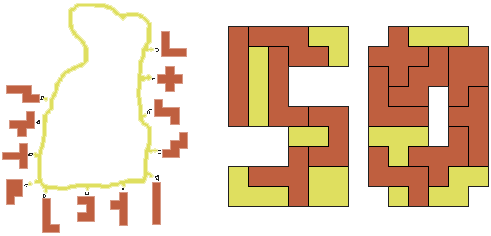
Peter Jeuken (Nederland) zocht het maximale aantal polyomino's 1 t/m 4 (die elkaar niet mogen raken) die in de 5 en in de 0 kunnen voorkomen. Met behulp van de computer vond hij een oplossing met 7 polyomino's in de 5 en een met 7 polyomino's in de 0.
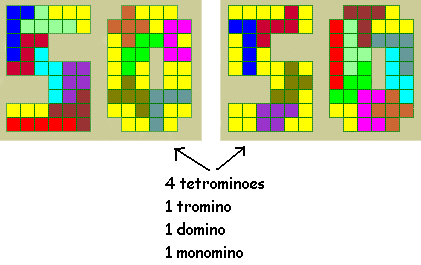
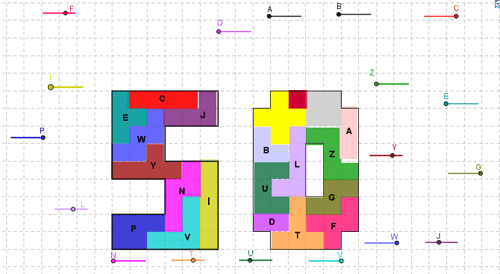
Peter Jeuken stuurde ons ook nog twee andere oplossingen. Zij zijn ontstaan uit een denkbeeldige discussie tussen twee puzzelliefhebbers.
De ene is Peet. Hij houdt van pentomino-puzzels op te lossen. Hij gebruikt enkel potlood en papier. De andere is Jeek. Hij houdt ervan computerprogamma's te schrijven. Eťn van zijn programma's dient om perfecte vuloplossingen te vinden in een vooraf gedefinieerd veld.
Na een week komen ze elk met een oplossing.
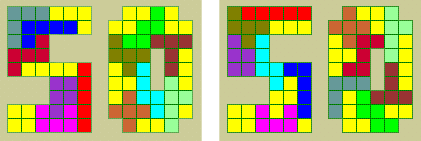
Kan je raden welke van Peet is en welke van Jeek?
Dario Uri mailde:"The problem of Kate admits a lot of solutions, I have chosen this because it is the only one that I have found where in the number 5 there are seven pentominoes, in all the other solutions the pentominoes are separated six and six for the two figures 5 and 0."
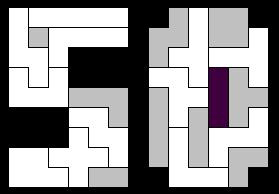
Peter Esser mailde:"Fixing some of the smaller polyominoes at places in the '5' by hand, the computer could finish the whole pattern immediately.The third solution met all conditions."
En verder: "I'm sorry to hear that this is the last competition; it was alwas great fun and I appreciate your work very much. Thanks a lot."
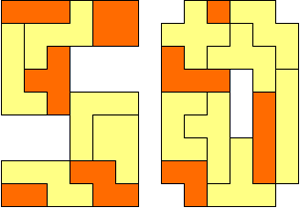
De volgende oplossing is van Frank Tinkelenberg.
De kleine stukken zijn gearceerd, zodat je makkelijk ziet dat ze elkaar niet raken.

Helmut Postl mailde: "It was not too difficult to find a solution by hand. The many small pieces provide a lot of varieties."