51. NWD 2016-wedstrijd
Na een paar jaar rust komt er toch opnieuw een wedstrijd.
Het verlangen naar de leuke contacten werd te groot en het geven van een workshop op NWD 2016 is een uitstekende gelegenheid.
De naam van onze workshop

Hij lijkt op onze eerste wedstrijd en op de zeventiende wedstrijd (Je kan daar ook bij records naar de oplossingen kijken)

Je neemt alle pentomino's die de ontvouwing zijn van een leeg doosje.
Voor deze opdracht maakten we een document dat je hier kan downloaden.

Maak met deze pentomino’s een omheining met een zo groot mogelijke ingesloten oppervlakte. 
De pentomino’s moeten in één vlak liggen en elkaar raken met minstens 1 zijde.

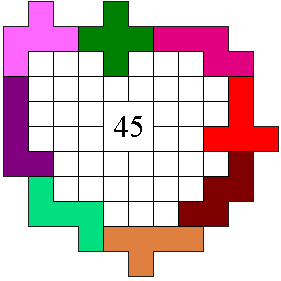
In het voorbeeld zijn er 45 eenheidsvlakjes ingesloten.
Gelukt?
Probeer nu ook te zorgen dat figuur gevormd door de buitenomtrek van de omheining een symmetriemiddelpunt bezit d.w.z. door draaiing rond dit punt over een hoek van 180° moet de figuur op zichzelf afgebeeld worden.

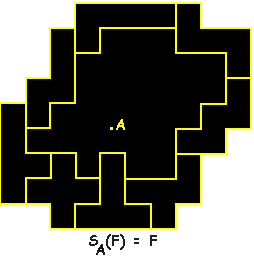
In het voorbeeld zijn er 30 eenheidsvakjes ingesloten. Het is de bedoeling van zoveel mogelijk vakjes in te sluiten.

Om te merken dat betere resultaten verkregen worden door met de pentomino's  een cirkelvormige figuur te maken zijn 8 pentomino's nogal weinig.
Verklaring: de cirkel is de vlakke figuur die met éénzelfde omtrek de grootste oppervlakte heeft.
Daarom maken we een gelijkaardige opgave met de eenzijdige pentomino's die de ontvouwing van een doosje zijn.


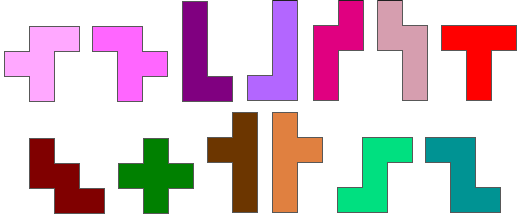
Maak met deze pentomino’s een omheining met een zo groot mogelijke ingesloten oppervlakte. 
De pentomino’s moeten in één vlak liggen en elkaar raken met minstens 1 zijde. (Je mag de vormen niet spiegelen!)
Dit deel van de wedstrijd lijkt op wedstrijd 24.

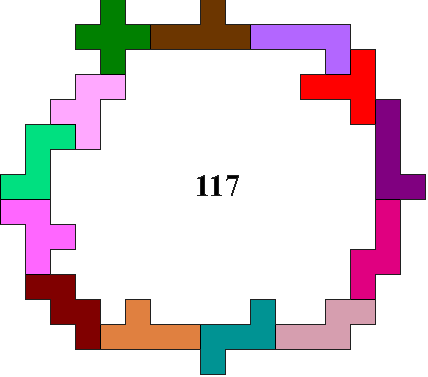
In het voorbeeld zijn er 117 eenheidsvlakjes ingesloten.
Gelukt?
Probeer nu ook te zorgen dat figuur gevormd door de buitenomtrek van de omheining een symmetrie-as bezit d.w.z. door spiegeling in de rechte moet de figuur op zichzelf afgebeeld worden.

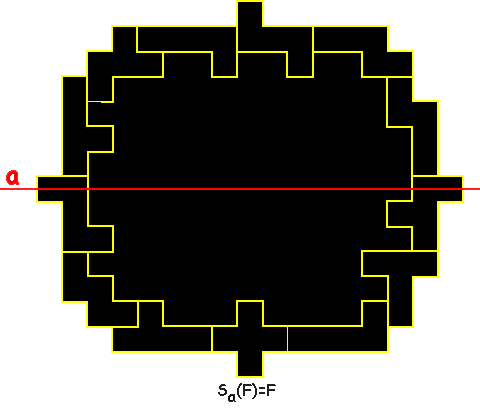
In het voorbeeld zijn er 120 eenheidsvlakjes ingesloten.

Een uitstekende hulp bij het zoeken naar een oplossing is het programma “FlatPoly2”. Je kunt het downloaden op de homepagina van Aad van de Wetering, Driebruggen. Speciaal voor onze wedstrijd voegde hij "PentoOneSide.fpo" toe.
Bedankt Aad.

We kunnen een gelijkaardige opgave maken met hexomino's.
Je neemt alle hexomino's die de ontvouwing zijn van een kubus.
Voor deze opdracht maakten we een document dat je hier kan downloaden.

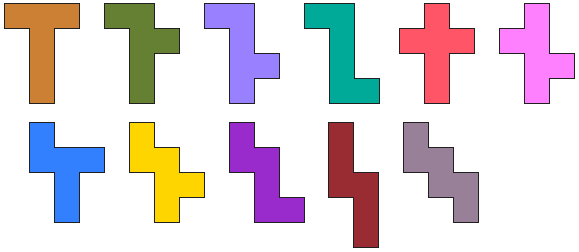
In onze wedstrijd 19 werkten we ook met deze hexomino's.
Maak met deze hexomino’s een omheining met een zo groot mogelijke ingesloten oppervlakte. 
Deze hexomino's moeten in één vlak liggen en elkaar raken met minstens 1 zijde.


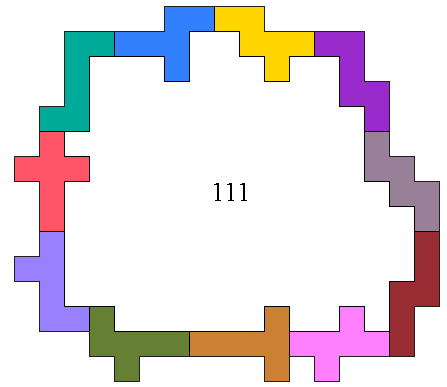
In het voorbeeld zijn er 111 eenheidsvlakjes ingesloten.