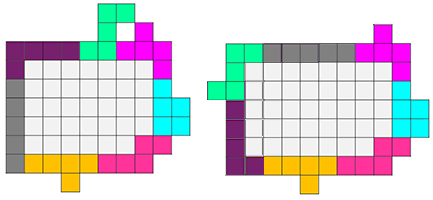
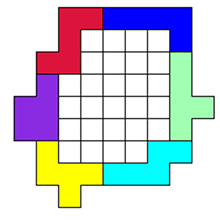
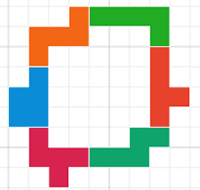
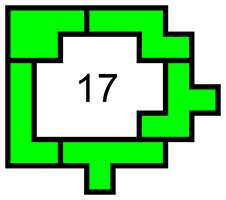
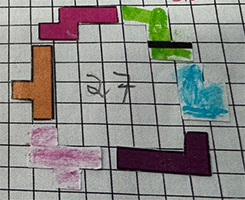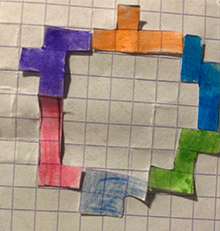Er staat nergens in de voorwaarden dat de pentomino’s in één vlak moeten liggen, dus

Op deze manier kunnen er 37 vierkantjes ingesloten worden.
De klassen van Fiona Lamb van het
Guldensporencollege Kaai 2 Kortrijk
Vierdes CLIL (wiskunde in het Engels, vanuit Grieks-Latijn, Latijn en
Natuurwetenschappen).
|
|
|
|
|
|
Vierdes uit Toerisme
en Taal & Communicatie
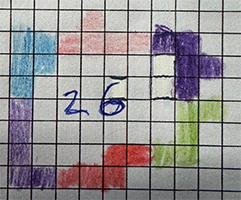
Het beste groepje Noémie Desmet en Megna Kumar.
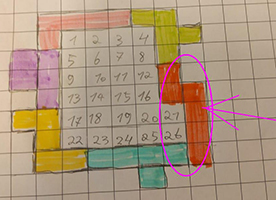
Ook een goede poging - ze konden 26 vakjes insluiten.

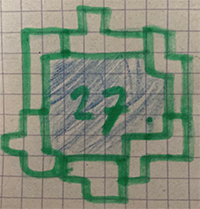
Vierdes uit de richting Bedrijf & Organisatie.
Mohamed Labed (27) was zo trots om de beste van de klas te zijn!

"Bedankt voor de leuke wiskundepuzzels."
Van Ilse Vanpoucke kregen we volgend bericht:
"Met enkele klassen van het Guldensporencollege Kaai2 zijn we de nieuwe
uitdaging aangegaan. Enkele groepjes slaagden erin om met zes pentomino’s een
omheining te maken en zo 26 eenheidsvakken in te sluiten. De leerlingen waren
heel gemotiveerd en amuseerden zich met deze opdracht. Het was een leuke
afwisseling in de les wiskunde.
|
|
|
|
Van de leerlingen van Christoph Bonte uit de
Sint-Jozef Humaniora Brugge
De volgende keurden we af:
De klassen van Matthias Maes uit
't
Saam Campus Aloysius Diksmuide.

Er werd hard gezocht.
Leerlingen die het lukte om meer dan 24 vakjes in te sluiten:
Matthias Capper, Stan Bonte, Fien Billiet, Lisa Vanhaverbeke en Laura Logghe.
We vinden het vooral belangrijk van naar de gevonden omheining te kijken en soms
nog meer vierkantjes te kunnen insluiten door sommige pentomino's te draaien of
te spiegelen.



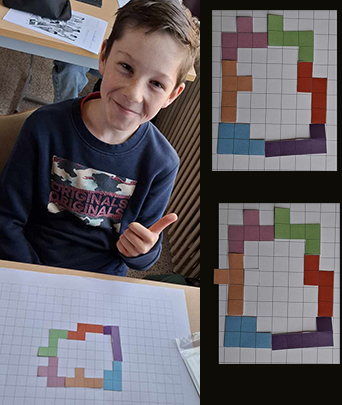

"Bedankt voor de leuke wiskundepuzzels. Onze leerlingen hebben al hun hoofd
erop gebroken. 😉
Momenteel komen we bij de pentomino's niet verder dan 26. Is een tip
mogelijk om beter te kunnen doen?"
We hadden niet echt een tip, eens proberen in andere volgorde.

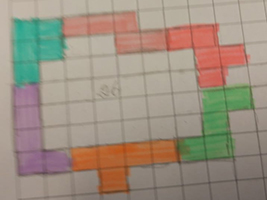
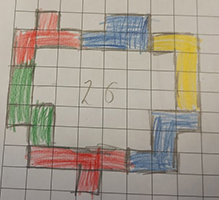
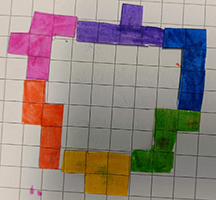
Filip Geeurickx uit het
Sint-Angela in Ternat
We kregen van Filip de volgende inzendingen:
|
|
|
|
Ze bleven maar zoeken. Jef wou oorspronkelijk de pentomino's niet draaien.
(Werkte dus met enkelzijdige pentomino's).
Ze vonden er alledrie eentje van 27. Knap gedaan!
|
Jef
|
Simon |
Phileas |
Els Vandenbussche stuurde een oplossing van 25 ingesloten vierkantjes.

P en Z wisselen levert hetzelfde resultaat, maar P draaien levert één meer.
Van Yana Vander Rasieren kregen we een maximale oplossing van 27. Proficiat!
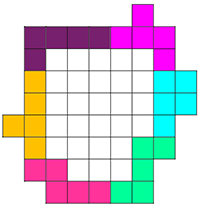
Eerst kregen we een oplossing van 34. Ze had echter ook de I-pentomino gebruikt. Op die manier kunnen we er 39.
Kan jij nog beter?