
Onze leerlingen van het 2e jaar T.I.D. Ronse België waren heel blij met de inzendingen.

We kregen een maximum oplossing van 43 van:
| Andrew Clarke | Australië |
| Jonah P. DeWall | USA |
| Kate Jones | USA |
| Paul Kunkel | USA |
| Javier Ospina | Colombia |
| Esther Pluess | Zwitserland |
| Helmut Postl | Oostenrijk |
| Andreas Rottler | Duitsland |
| Jaap Scherphuis | Nederland |
| Ton Tilllemans | Zwitserland |
| Pieter Torbijn | Nederland |
| Aad van de Wetering | Nederland |
| Hein van Winkel | Nederland |
| Andreas Zollner | Duitsland |
|
Fréderic Ysebaert |
België |
Op 24 mei 2001 kregen we de volgende email toegestuurd:
“Hello, our names are Katie Hagara and Ashley Reynvaan. We live in Aberdeen, Washington, U.S.A. We are both in 10th grade at Aberdeen High School, and have been working on this project for 2 weeks. With the help from our Geometry teacher, Mr. Kunkel, we were able to match the 36 squares in each region. Yet we are still working on figuring a larger number into the regions.”
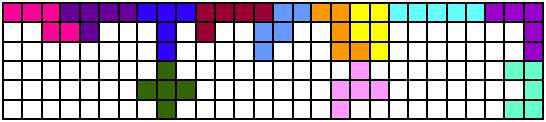
Een betere oplossing hebben we niet ontvangen.
Op 25 mei 2001 kregen we nog een e-mail:
“This is my pentomino project from my geometry class...... My teacher is Mr. Kunkel..... We did this project based on your contest so we are sending it in when we have completed it... My name is Elise Pier and I’m a freshman this year and in the geometry class..... so I hope you like it Thanks for taking time to look it over.... Elise Pier”
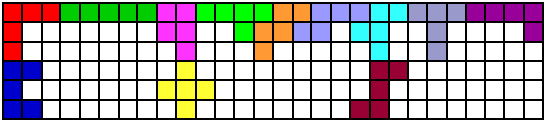
We vinden het inderdaad leuk van oplossingen van leerlingen te krijgen, ook al zijn ze niet maximaal.
Samen met zijn inzending van 43 stuurde Andrew Clarke ons zijn analyse van het probleem.
Hij maakt een sliert van pentomino’s en komt tot een lengte van 41.
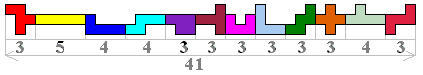
Hij voegt er 9 bij omdat de balustrade 3 balusters heeft en komt dus tot een totaal van 50, die moet gebruikt worden voor 3 hoogten en een breedte.
Volgens ons beschikt men niet over 50 vierkantjes maar heeft Andrew geen rekening gehouden met het feit dat de buitenomtrek van de balustrade een rechthoek moet zijn.
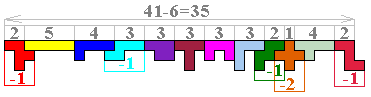
De pentomino’s waar men verliest, kan men in onderaan in de 2 binnenste balusters plaatsen maar daarvoor heeft men er doorgaans maar 4 nodig.


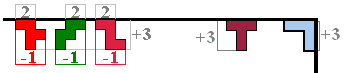
Na het bekijken van alle vormen voor de balustrade te maken komen we tot het feit dat men in de meest gunstige legging tot maar beschikt over 49 bruikbare eenheden.
We merken op dat in dat geval de V-pento zeker in de hoek van de balustrade moet en de T-pento moet zeker bovenaan een andere baluster geplaatst worden.
De meest gunstige keuze (als onze balustrade meer dan 6 hoog is) voor de pentomino’s onderaan de 2 midden-balusters is X,F,Z en W. Er blijven dan voor de buitenomtrek 35-7+3=31 vierkantjes over (+3 komt van de V-pento).
Als we de balustrade 9 hoog maken zouden we verwachten dat ze 22 lang kan zijn, maar met pentomino’s weet je nooit.Wat we ook doen we verliezen altijd 1 eenheid.
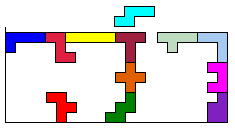
Onze recordbalustrade is dus 9 hoog en 21 breed.Aantal lege vakken is dus 9x21-60=129.
In elk deel zijn er dus 129:3=43 ingesloten vierkantjes.
Als we de balustrade 8 hoog maken kan ze hoogstens 31-8=23 breed zijn. In dit geval is het aantal lege vierkantjes 8x23-60=124. Dit is al minder dan ons record maar we merken bovendien op dat het niet deelbaar is door 3.Bij een hoogte die geen drievoud is moet de breedte dus een drievoud zijn.
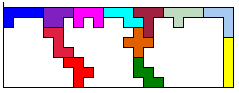
Eén van mijn leerlingen merkte op dat we bij een hoogte van 8 ook een baluster konden maken met de L- en N-pentomino. In dat geval was er echter op de buitenomtrek een verlies van 1
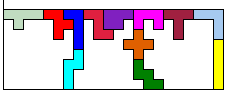
Als we een balustrade maken met hoogte 7 en we willen minsten per vak 43 ingesloten vierkantjes dan moet de breedte 27 zijn omdat (43x3+60):7=27.
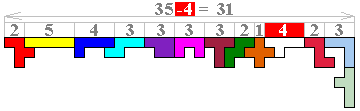
Op de tekening merken we dat we dus maar 4 eenheden uit de breedte mogen wegnemen om de 2 binnenbalusters te maken. Dit is niet mogelijk.
Bij een balustrade met hoogte 6 en met minstens 43 ingesloten vakjes moet de breedte 32 zijn omdat (43x3+60):6=31,5
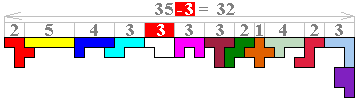
We zouden dus niets uit de breedte mogen nemen om de balusters te maken.
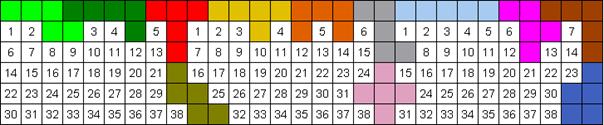
Op 28 mei 2001 kregen we van Paul Kunkel, meetkundeleraar van Ashlay, Katie en Elise de maximum oplossing van een balustrade met hoogte 6 toegestuurd.
Bij een hoogte van 10 moet om het record te breken de breedte 19 zijn want (43x3+60):10=18,9. Omwille van de deelbaarheid door 3 moet de breedte dus 21 zijn.
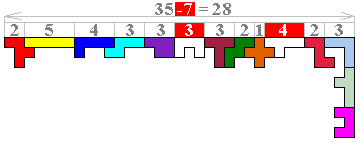
Uit de breedte van 28 mogen we maar 7 eenheden wegnemen om de 2 binnenbalusters van 10 hoog te maken. Dit gaat niet.
Voor de andere hoogten zetten we onze redenering op dezelfde manier verder.
Besluit:
De maximale oplossing vinden we bij een balustrade van 9 hoog en 21 lang (Het ingesloten aantal vierkanten per deel is dan 43)
Van Roel Huisman kregen we een ruimtebalustrade. Het verband met onze wedstrijdopgave is ver zoek maar de vindingrijkheid van Roel is groot! Het geeft ons een idee voor een volgende wedstrijd.
Roel mailt: “Met slechts 4 pentomino’s kun je al gemakkelijk 36 vierkantjes insluiten. De drie viewpoints laten steeds een balustrade zien met een rechthoekige buitenkant.Ik heb verder niet nagedacht over een grotere omgesloten ruimte”