After a couple of years of silence yet again a contest.
The longing for the nice contacts became too strong and giving a workshop on NWD2016 provides an excellent opportunity.
The name of the workshop

It resembles our first contest and the seventeenth contest. (You can find the solutions at the Records.)

Take all pentominoes which are the unfolding of an empty box.
For this task we made a document which can be downloaded
 here

Form with these pentominoes an enclosure maximizing the enclosed area.
The pentominoes should lie in one plane and mutually have side contact.


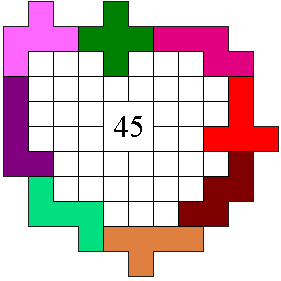
In the example 45 squares are enclosed.
Did you succeed?
Next try to achieve that the figure formed by the outer circumference of the enclosure has a point of symmetry, i.e. rotation around this point over 180 degrees leaves the figure unchanged.

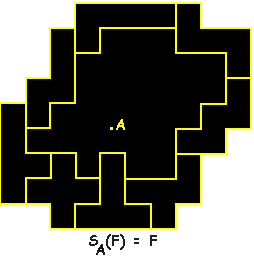
In the example 30 squares are enclosed. Obviously you should strive to enclose as many as possible squares.
Observing that better results are reached by forming a circular figure with the pentominoes, 8 pentominoes appear to be rather few for that purpose.
Explanation: the circle is the unique figure which for fixed circumference has maximal area.
Therefore we offer a similar task with the one-sided pentominoes which are the unfolding of a box.



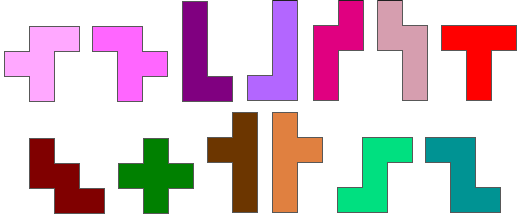
Form with these pentominoes an enclosure with maximal enclosed area.
The pentominoes should lie in one plane and mutually have side contact. (You are not allowed to mirror them!)
This part of the contest resembles contest 24.


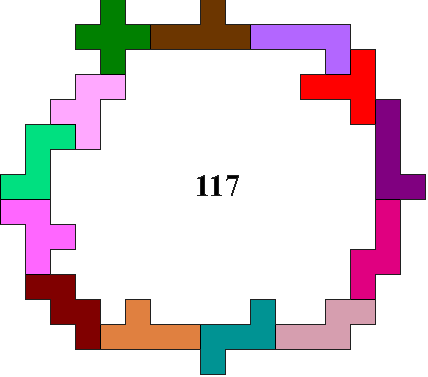
In the example 117 squares are enclosed.
Did you succeed?
This time try to achieve that the figure formed by the outer circumference of the enclosure has an axis of symmetry, i.e. mirroring the figure in this axis leaves it unchanged


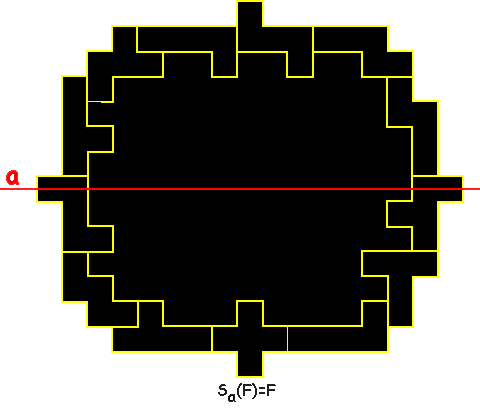
In the example 121 squares are enclosed.

An excellent help in searching for a solution is the program “FlatPoly2”. You can download it from the home page of Aad van de Wetering, Driebruggen. Especially for our contest he added “PentoOneSide.fpo”.
Thank you Aad


Finally we offer a similar task with hexominoes.
Take all hexominoes which are the unfolding of a cube.
For this task we made a document which can be downloaded
 here.

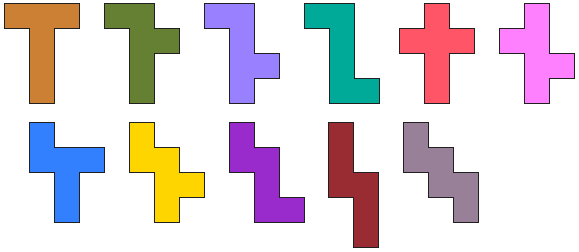
The nineteenth contest was also about hexominoes.
Form with these hexominoes an enclosure maximizing the enclosed area.
The hexominoes should lie in one plane and mutually have side contact.



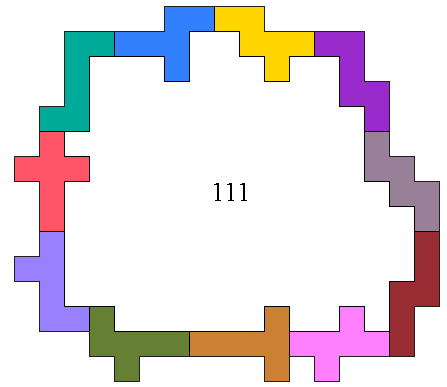
In the example 111 squares qare enclosed.

Texas Instruments grants us a  TI-84 Pus CE-T.