Nous avons réalisé ce concours à l’occasion des  NWD2016
Il ressemble à nos concours 1 et concours 17 (Vous pouvez aussi y voir les solutions)

Prenez tous les pentominos dont la forme permet de réaliser une petite boîte ouverte.
Pour cette consigne, il y a un document à télécharger
ici


A l’aide de ces pentominos, réalisez une clôture qui encercle le plus grand nombre de cases possible. 
Les pentominos doivent être sur le même plan et se toucher par au moins un côté.


IDans cet exemple, 45 cases sont enfermées.
Ça marche?
Essayez d’obtenir que la figure ait un centre symétrique: si on la tourne à 180° autour de ce centre, on doit obtenir son reflet.

Dans cet exemple, 30 unités sont encerclées. Il faudrait qu’il y en ait un maximum.

Huit pentominos ne sont pas suffisants si on veut démontrer qu’on obtient de meilleurs résultats en réalisant une figure en forme de cercle.
Pourquoi? Le cercle est la figure plane qui a la plus grande surface pour la même circonférence.
Nous proposons donc une consigne semblable à réaliser avec les pentominos à une face qui permettent de fabriquer une petite boîte ouverte.

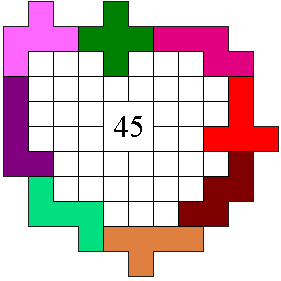
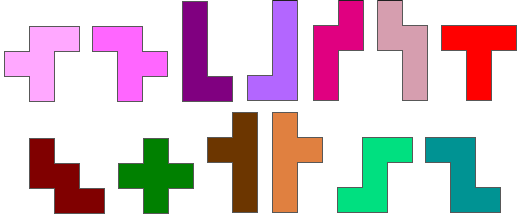
A l’aide de ces pentominos, réalisez une clôture qui ait une surface encerclée maximale.
Les pentominos doivent être sur le même plan et se toucher par au moins un côté. Cette partie du concours ressemble au concours 24.



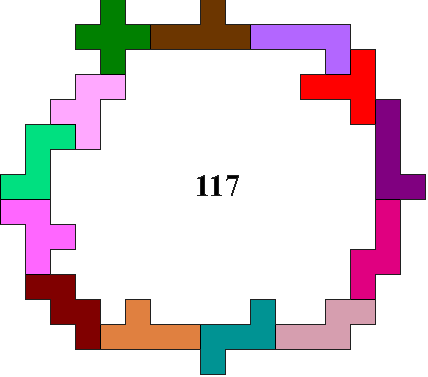
Dans cet exemple 117 cases sont encerclées.
Ça marche?
Essayez d’obtenir que la figure ait un axe de symétrie: l’une moitié de la figure doit se réfléchir dans l’autre.


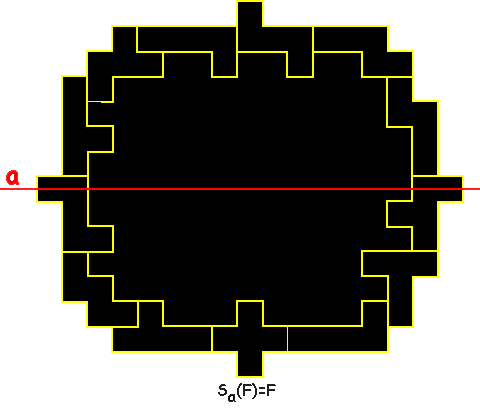
Dans cet exemple 120 cases sont encerclées.


Le programme "FlatPoly2” peut vous aider à trouver une solution. Vous pouvez le télécharger sur le site d’Aad van de Wetering, Driebruggen. En vue de ce concours, il y a tout spécialement ajouté le "PentoOneSide.fpo".
Merci Aad.



On peut faire une même consigne pour les hexominos.
Prenez tous les hexominos qui permettent de réaliser un cube.


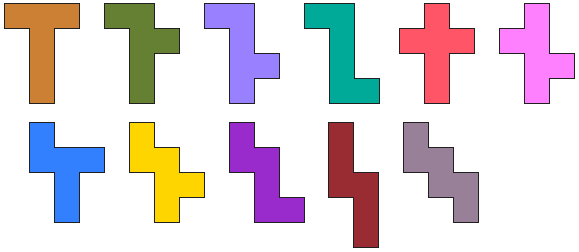
En vue de cette consigne, nous avons créé un document téléchageable ici.

Nous avons également utilisé des hexominos dans notre concours 19.
 A l’aide de ces hexominos, réalisez une clôture d’une surface maximale. 
Les hexominos doivent être sur le même plan et se toucher par au moins un côté.




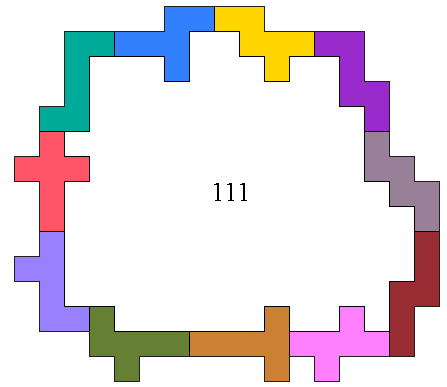
Dans cet exemple 111 cases sont encerclées.