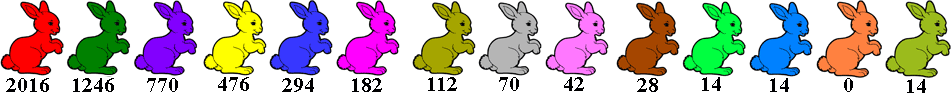2016

Martin Kindt mailde "Ik wens jou het allerbeste toe in het driehoeksjaar 1 + 2 + 3 + ... 62 + 63" en inderdaad 2016 is een driehoeksgetal.
63x64:2 = 2016
Een driehoeksgetal is een type veelhoeksgetal. Een driehoeksgetal kan grafisch worden weergegeven door het aantal stippen in een gelijkzijdige driehoek, die gelijkmatig met stippen wordt gevuld.
We maakten hiervan een voorstelling en wensen dat 2016 even kleurrijk mag zijn.

De basis heeft 63 vierkantjes en in het totaal zijn er 2016 gekeurde vierkantjes.
Wil je een driehoek om zelf in te kleuren? Mail dan naar o.d.m@fulladsl.be

Matthijs Coster mailde: "Het is ook een zeshoeksgetal"
Een zeshoeksgetal is een geheel getal, dat gevonden kan worden als het aantal punten van gezamenlijke zeshoeken met een gemeenschappelijk hoekpunt en (gedeeltelijk) twee gemeenschappelijke zijden, en met een telkens oplopend aantal punten per zijde.
De formule om de zijde te vinden is 2n² - n
2016 = 2. 32² - 32
We maakten ook hiervan een voorstelling en kleurden de 2016 vakjes in.

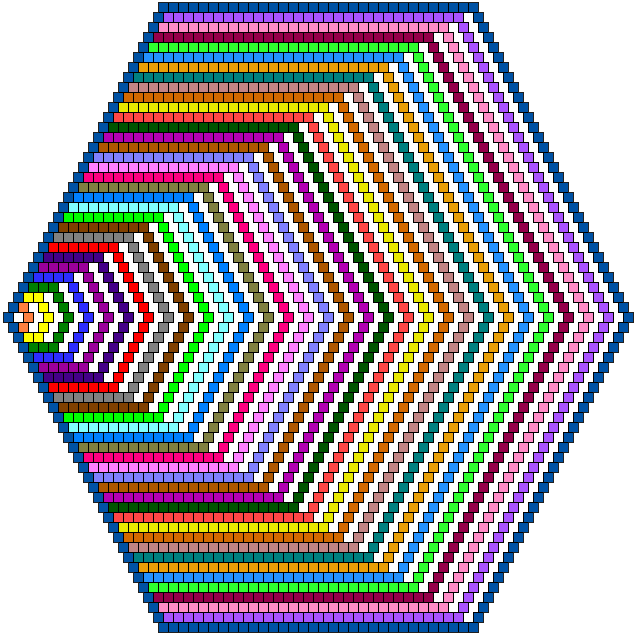
Wil je deze tekening om zelf in te kleuren? Mail dan naar o.d.m@fulladsl.be

Voor "nos amis francophones" maakten we de volgende tekening met een horizontale symmetrie-as en een 2016 vol "de JOIE"
Onze tekening heeft juist 2016 gekleurde vlakjes. De zijde van de buitenste zeshoek is 27 en van de binnenste 7.
Gekleurde vakjes is 6x(26+25+24+...+8+7+6) = 6x32x21:2 = 2016

We willen nog eens benadrukken (omdat we het zeer leuk vinden - gevonden op youtube) dat het spiegelbeeld van 2016 in de rechte a "joie" is.


Onze schattige aapjes die we gaan gebruiken in onze workshop op NWD dienden eerst voor ons nieuwjaarskaartje.

2016 is tenslotte "het jaar van de aap"
Hopelijk ben je aan het einde ook apetrots op je prestaties in 2016

Wat je natuurlijk jaarlijks kan aanpassen is onze rekenrups.
In 2005 wonnen we met 3EE hiermee de klassenklus van Volgens Bartjens

De reeks begint met het jaartal en bestaat uitsluitend uit positieve getallen. Het volgende getal is steeds het verschil van de twee voorgaande.
De opdracht: zorg dat de reeks zolang mogelijk is.
 Je kan hiervoor een exelblad maken.
De uitwerking (en bewijs) kan je in het document vinden.
Fibonacci is de sleutel.

Voor 2016 is het wel een lange reeks: 14 getallen en 14 komt driemaal voor en ze eindigt op 14

En dan nog 2016 als som van machten:






Jan van de Craats mailde: "Tel alle ballen"

(4² + 5² + 6² + 7²) x 16