
We vonden de inspiratie voor deze vraag bij de Vlaamse Wiskunde Olympiade
2000-Eerste ronde.Op elk vierkant met zijde 1 van de pentomino wordt een regelmatige zeshoek geconstrueerd met hetzelfde middelpunt als het vierkant. Bepaal de blauwe oppervlakte.

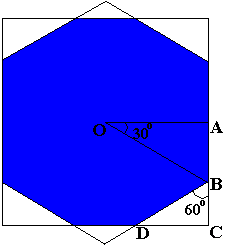
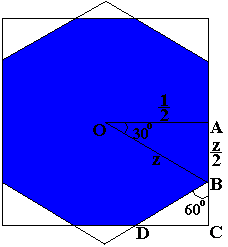
Eerst bepalen we de zijde z van de zeshoek via
driehoek OAB:
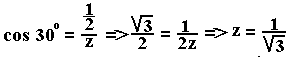
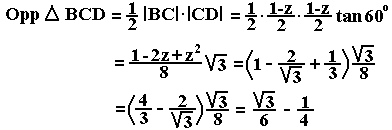
De oppervlakte van één vierkant - 4 oppervlakte Δ BCD is:
![]()
De oppervlakte van het blauwe gedeelte is:
![]()