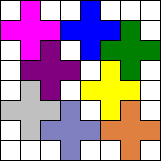
We kregen deze vraag van Toshi Kato uit Japan: hoeveel X-pentomino's kan je leggen in een vierkant van 8x8?
We gingen onmiddellijk aan de slag.
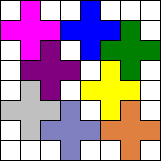
Het leek ons heel eenvoudig, te simpel voor een
vraag uit Japan.
Het antwoord luidde dan ook: "ik kan er 9 "
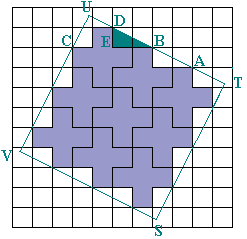
We vroegen raad aan Aad en hij gaf ons het sleutelwoord: "DRAAIEN"
Kan je het vinden?
Oplossing
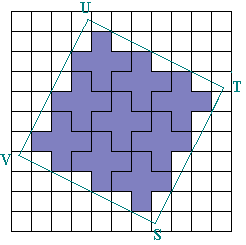
Bewijs
1. We maken gebruik van de
vergelijkingen van rechten, hun snijpunten en de afstanden.
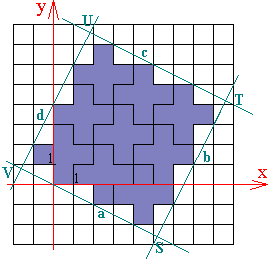 a <—> y = - ½ x b <—> y = 2 x - 13 c <—> y = - ½ x + 8,5 d <—> y = 2 x + 4 |
Aan de richtingscoëfficiënten van de rechten merken
we dat VSTU een rechthoek is.
Door het oplossen van stelsels kunnen we de coördinaten van de hoekpunten
bepalen en vinden we:
V(-1,6; 0,8) ; S(5,2;-2,6) en T(8,6; 4,2)
Door middel van deze coördinaten kunnen we de lengte van [ VS ] en [ ST ]
bepalen :
![]()
2.Steunen op gelijkvormige driehoeken (Thijs
Notenboom)

.