Het idee van het probleem is van Aad Thoen uit Nederland.
Aad van de Wetering mailde het probleem:
"Kan jij met zes pento’s zes andere pento’s omsluiten? Een hele set gebruiken allicht en het geheel moet gatloos zijn."
We zochten en vonden de volgende oplossingen:

Toen we de oplossingen naar Aad stuurden kregen we als antwoord:
"Goed gevonden! Maar die stekels aan de kanten, die zijn niet mooi. In de voorwaarden heb ik dat niet aangegeven, maar dat had ik eigenlijk wel moeten doen."
Wat bedoelde hij?
Moet de buitenomtrek een rechthoek (10 op 6) zijn?
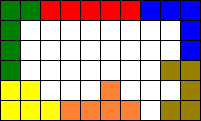
De boord van 24 vakjes kan niet gevuld worden met 6 pentomino's.
Moeten de omheinde pentomino's een rechthoek (6x5) vormen?
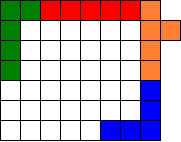
Om dit te doen hebben we zeker I,L,V en Y nodig. Zonder deze 4 pentomino's kan men geen rechthoek van 6X5 leggen.
Aad mailde:"Je kunt de stekeltjes toch ook naar binnen leggen? Rechthoeken zijn inderdaad onmogelijk."
We dachten dat we oplossingen gevonden hadden:
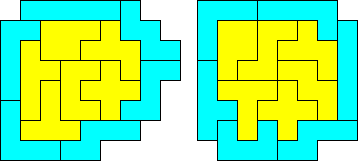
Maar alle oplossingen werden afgekeurd.
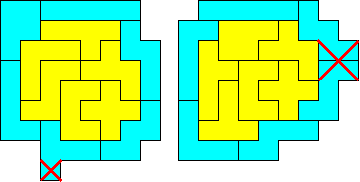
"De omtrek moet een sliert (of lint) zijn waarbij elke pentomino met de volgende maar één zijde (van een eenheid) gemeen heeft."
Eindelijk vonden we een goeie oplossing.

Aad van de Wetering zond ons twee oplossingen.
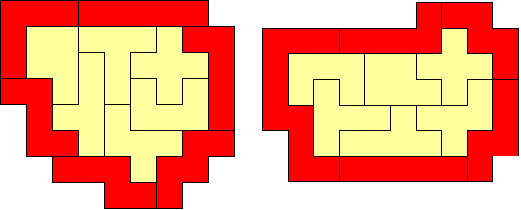
Onze oplossing lijkt aardig op die van Aad, nochtans hadden we niet gespiekt.
Aad Thoen, van wie het idee afkomstig is, mailde oorspronkelijk twee oplossingen.
Deze oplossingen hebben dezelfde buitenrand.
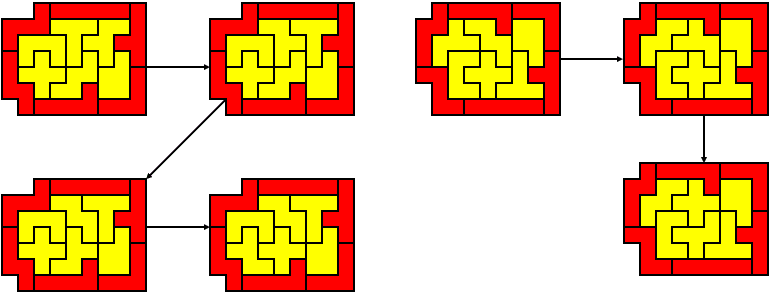
Aad Thoen stuurde ons nadien een mooi word-document waarbij een aantal oplossingen gevonden werden door verwisseling van een aantal pentomino's.
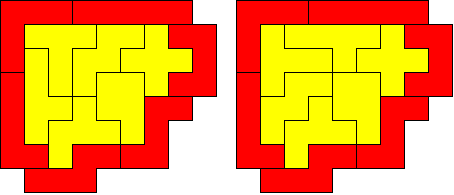
Variatie van de tweede oplossing van AvdW via cyclische verwisseling van V,W en Z.
Verwisseling in die oplossing van V en Z levert een vijfling op.

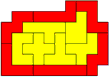
Variatie van de eerste oplossing van AvdW
V en Z verwisseld, een trio:

Nu Z en W verwisseld, nog een trio:
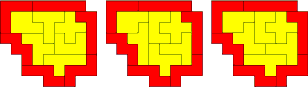
V,W en Z cyclisch verwisseld:
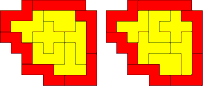
Geinspireerd door de vorige oplossingen (van Aad Thoen) vonden we er nog een paar:
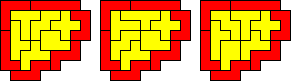
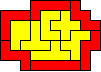
En toen kwam er een oplossing van Helmut Postl (Oostenrijk)
Hij vond 79 verschillende vormen die opvulbaar zijn met 6 pentomino's en die we kunnen omheinen met een slinger van de andere 6 pentomino's.
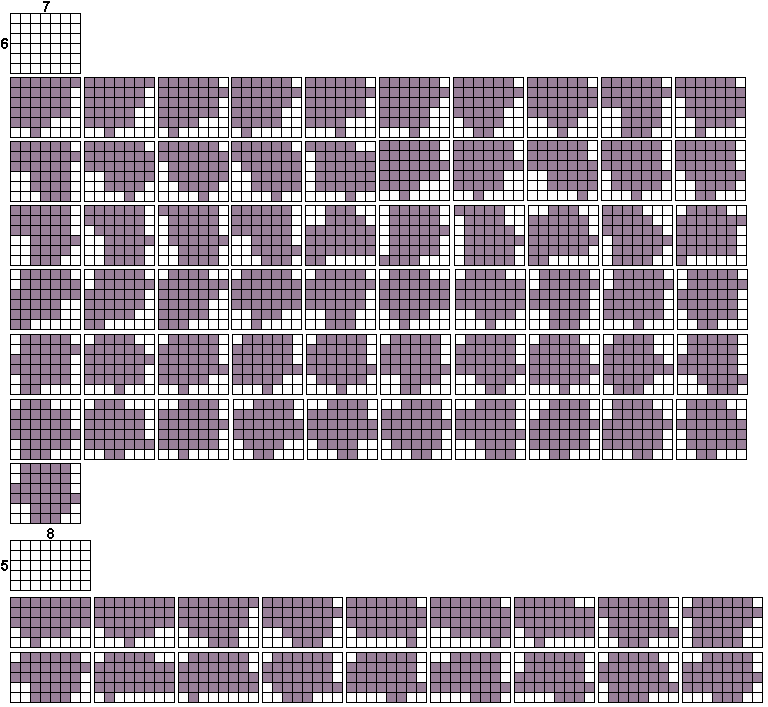
In totaal vond Helmut (zijn computer) 128 oplossingen.
Voor de slinger pentomino's zijn er vijf mogelijke combinaties:
ILNUVZ (47), ILNVWZ (57), INUVWZ (6), ILNUWZ (4) en ILNUVW (14)
Er is juist één vorm die twee verschillende combinaties als omheining heeft.
Wil je de oplossingen zien?
Druk hier
Bob Henderson vond nog een aantal andere oplossingen.
De eerste maal mailde hij:"Here are some new ways to enclose 6 pentominos using the other 6, without enclosing any empty spaces. I used a perimeter of 28 units instead of 30 units as shown in your examples of good solutions. The 6 outside pentominos include 2 unit squares inside (not outside) their perimeter, so I think they are not like your examples of incorrect solutions. I hope you like these results -- it was hard work to find them all!"
We vroegen Aad zijn mening en hij mailde: "De voorbeelden van Bob met Y in de omtrek zijn uiteraard niet juist. Maar iedereen mag zijn eigen spelregels maken."
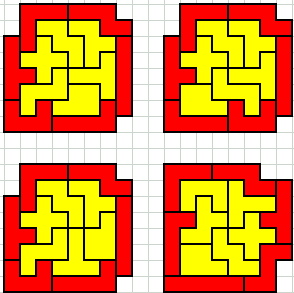
Four 8 by 8 Thoen solutions with perimeter = 28
Seven 9 by 7 Thoen solutions with perimeter = 28
Op 30 januari 2013 mailde Bob voor de tweede keer: "I found many solutions with 6 pentominoes (30 cells) on the perimeter. . . See the Excel attachment.
The solutions for 6 pentominoes with 28 cells on the perimeter and 2 cells inside are also interesting. I did not allow any 2x2 touching cells on the 6 border pentominoes for these 11 solutions.
I did not find any solutions with concave perimeters of 6 pentominos (30 cells). If you have seen these or any solutions to this problem that I have not found, please let me know!
Thank you for sharing this interesting puzzle"
Bob deelde zijn 128 oplossingen een beetje anders in namelijk in twee delen 9x8 en 10x7 oplossingen.
De slinger pentomino's ILNUVZ noemde hij Solutions for W inside (47)
ILNVWZ: Solutions for U inside (38 + 19)
INUVWZ: Solutions for L inside (6)
ILNUWZ: Solutions for V inside (4)
ILNUVW: Solutions for Z inside (6 + 8)
Bob stuurde zijn oplossingen toe in een exel-file. Je kan het hier downloaden