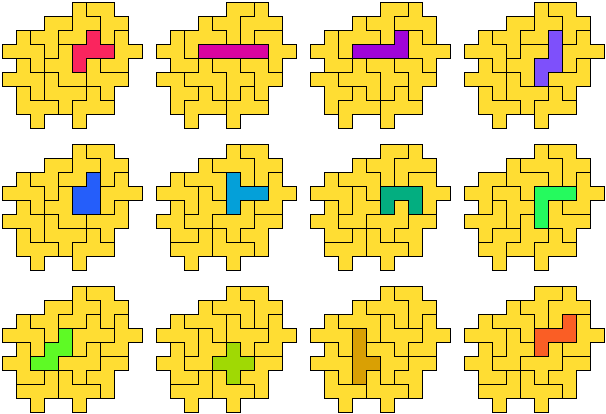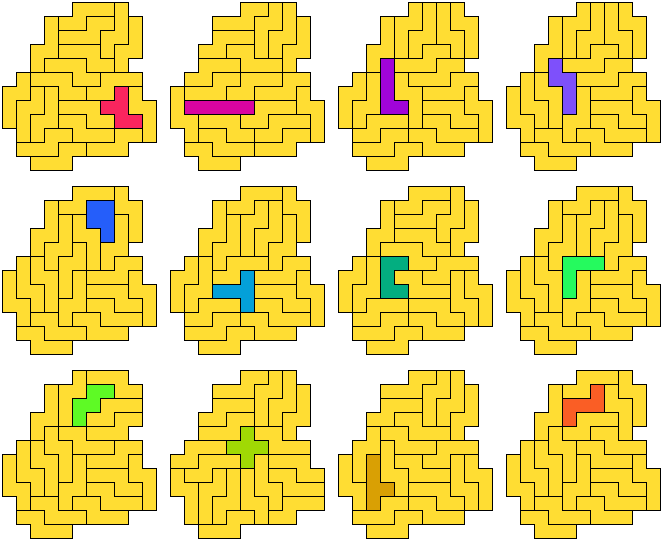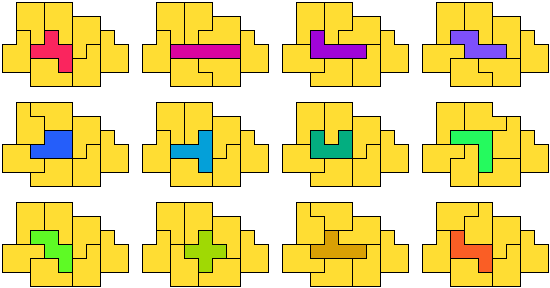Omringde pentomino in een congruente figuur
Livio Zucca
Toen we Livio Zucca het probleem van Aad Thoen 'omringde
pentomino in een rechthoek' toestuurden mailde hij terug:"I have a problem similar to yours: find the minimum shape containing all 12
pentominoes"
Livio (LZ) had meteen al twee oplossingen. Hij voegde er wel aan toe: "I
don't know if the solution is minimal"
L-pentomino (LZ)
De figuur bevat in totaal 15 pentomino's.

We kregen van George een oplossing in een vierkant maar waarbij het vierkant
bestaat uit 20 pentomino's.
We plaatsen de oplossing in een
variante van dit probleem.
P-pentomino (LZ)
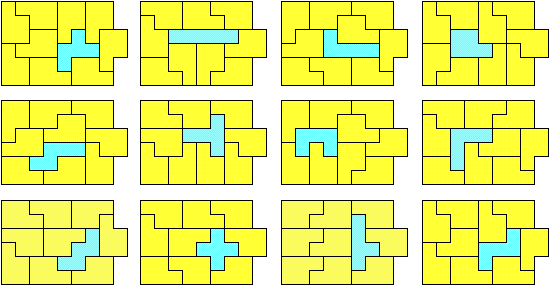
Nadien stuurde Livio een oplossing voor de F-pentomino met 36 pentomino's.

We kregen ook nog een gekarteld vierkant van Livio bestaande uit 53
pentomino's. We publiceerden dit bij een
vorig probleem
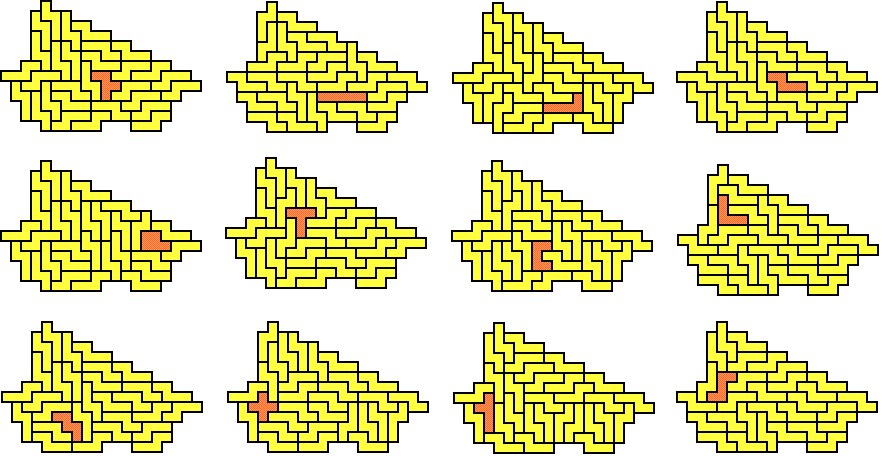
Livio stuurde ook een oplossing voor de N-pentomino: "My solutions are
very empirical, with no real method. Therefore there are probably smaller
solutions."
Inderdaad, George Sicherman vond er eentje van 19.
De figuur bevat in totaal 30 pentomino's.
Livio stuurde een oplossing voor de W-pentomino: "Here's another solution
to minimize :-) "
En ja hoor, George Sicherman vond er eentje van 26.
De figuur bevat in totaal 34 pentomino's.

We kregen van Livio ook een oplossing voor de Y-pentomino: "I'll send you
my solution for the Y-Pentomino before the Colonel minimize them. :-)"
Inderdaad, we kregen van George er één met 15 pentomino's.
De figuur bevat in totaal 30 pentomino's.

Aad van de Wetering stuurde ons een P-pentomino-oplossing waar de figuur 9
pentomino's bevat.
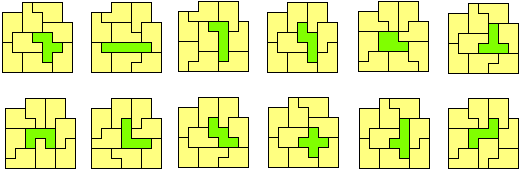
George Sicherman schoot in actie.
F-pentomino (GS)
De figuur bevat in totaal 12 pentomino's.
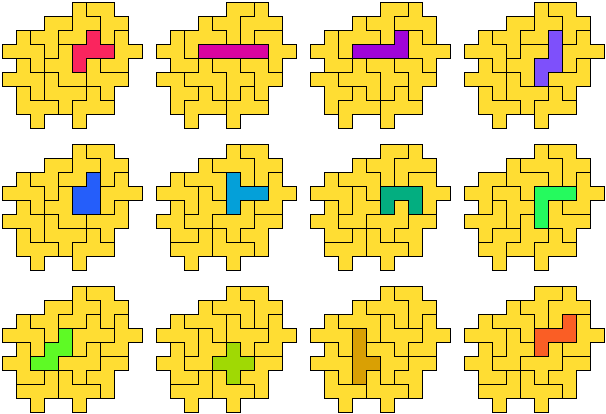
L-pentomino (GS)
De figuur bevat in totaal 14 pentomino's.
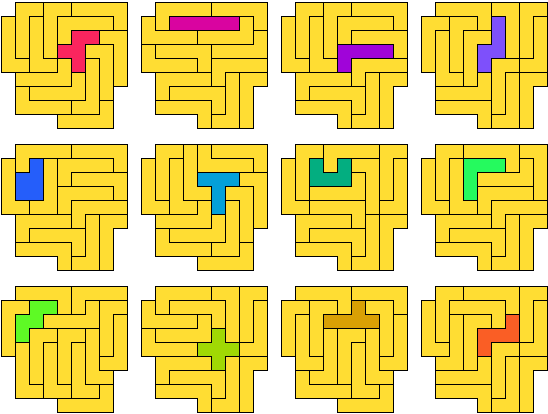
N-pentomino (GS)
De figuur bevat in totaal 19 pentomino's.
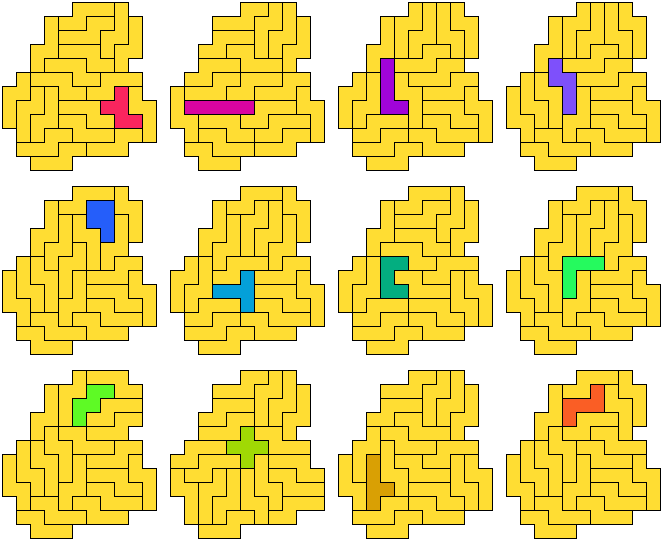
We kregen van George ook een oplossing in een gekartelde rechthoek maar
waarbij de rechthoek bestaat uit 42 pentomino's.
We plaatsen de oplossing in een
variante van dit probleem.
P-pentomino (GS)
De figuur bevat in totaal 8 pentomino's.
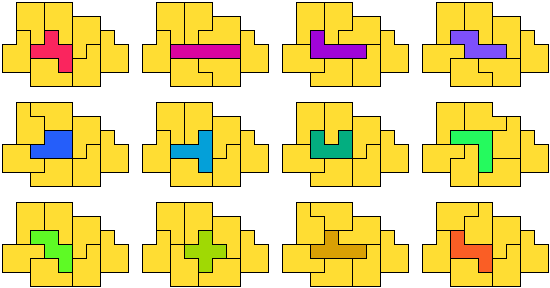
We kregen van George ook een oplossing in een rechthoek maar waarbij de
rechthoek bestaat uit 12 pentomino's.
We plaatsen de oplossing in een
variante van dit probleem.
W-pentomino (GS)
De figuur bevat in totaal 26 pentomino's.
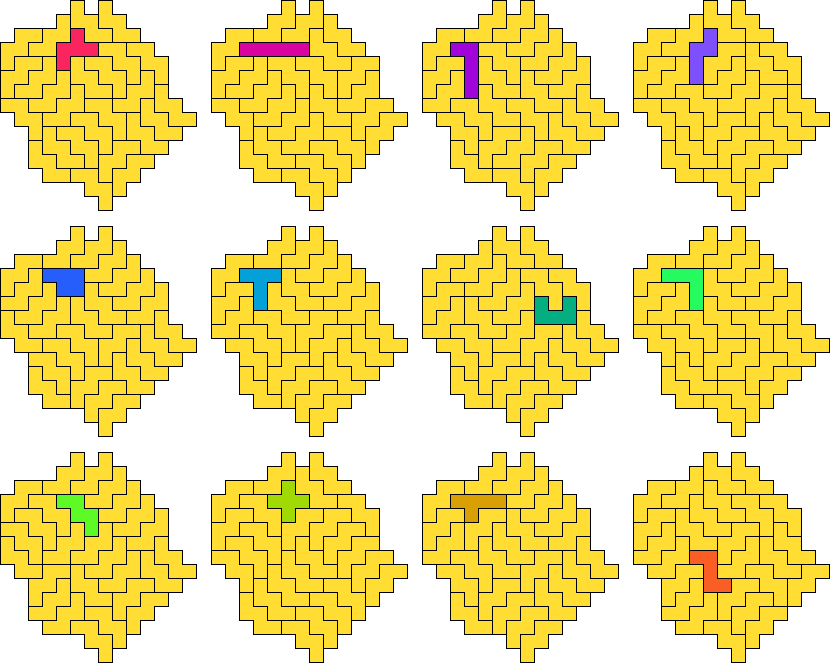
We kregen van George ook een oplossing in een gekartelde rechthoek maar
waarbij de rechthoek bestaat uit 40 pentomino's.
We plaatsen de oplossing in een
variante van dit probleem.
Y-pentomino (GS)
De figuur bevat in totaal 15 pentomino's.
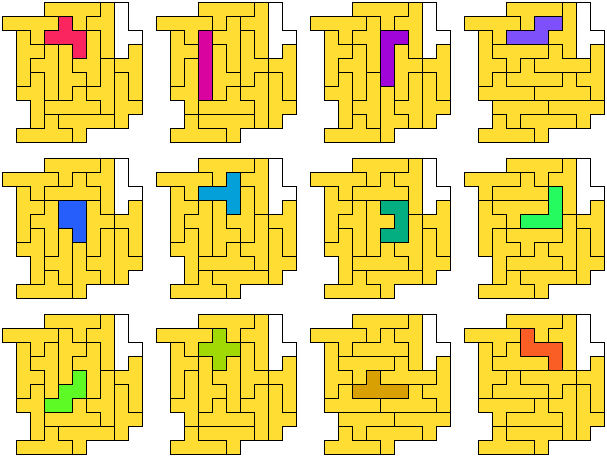
George stuurde eerst een oplossing met 16 pentomino's.
Om 14:24 uur kregen we de verbetering binnen. Livio Zucca had het ook
gezien. We kregen zijn bericht om 14:26 uur. (2 min later. Jammer)
We kregen van George een oplossing in een rechtoek maar waarbij de rechthoek
bestaat uit 40 pentomino's.
We plaatsen de oplossing in een
variante van dit probleem.
Livio Zucca stuurde het volgende:"With no pc :-)"
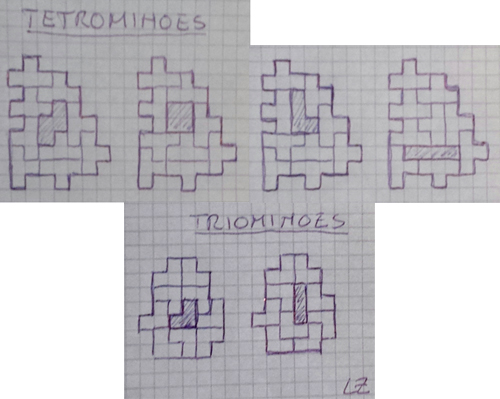
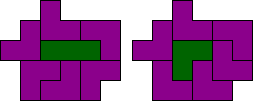
De tromino's kunnen we beter (ook zonder pc)
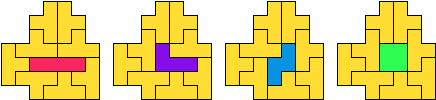
George Sicherman stuurde een betere oplossing met de tetromino's.
De figuur bevat maar 9 tetromino's.
Livio Zucca mailde: 'I think the missing tetromino is impossible for
parity problems."
George Sicherman zijn antwoord: "With polyominoes of even order greater
than 2, we shall always have parity problems."
Andere of betere oplossingen gevonden?