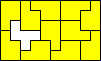
 10x6 (AT) |
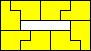 9x5 (AT) |
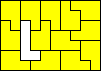 10x7 (AT) |
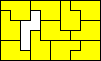 10x6 (AT) |
 6x5 (AT) |
 7x5 (AT) |
 10x6 (AT) |
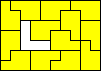 10x7 (AT) |
 10x6 (AT) |
 5x5 (AT) |
 7x5 (AT) |
 7x5 (AT) |
Van George Sicherman (GS) kregen we één omringde pentomino met I-pentomino's

7x5 (GS)
Van George Sicherman (GS) kregen we de oplossingen met de L-pentomino
behalve die rond de L.
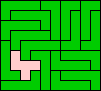 10x9 (GS) |
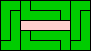 9x5 (GS) |
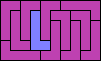 10x6 (OM) |
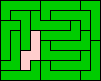 10x8 (GS) |
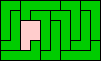 10x6 (GS) |
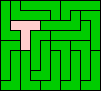 10x9 (GS) |
 10x6 (GS) |
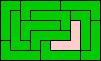 10x6 (GS) |
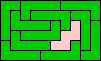 10x6 (GS) |
 5x5 (GS) |
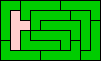 10x6 (GS) |
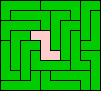 10x9 (GS) |
Van George Sicherman kregen we voor een
variant van dit probleem de volgende
oplossing toegestuurd.
De zijde van het vierkant is 10.
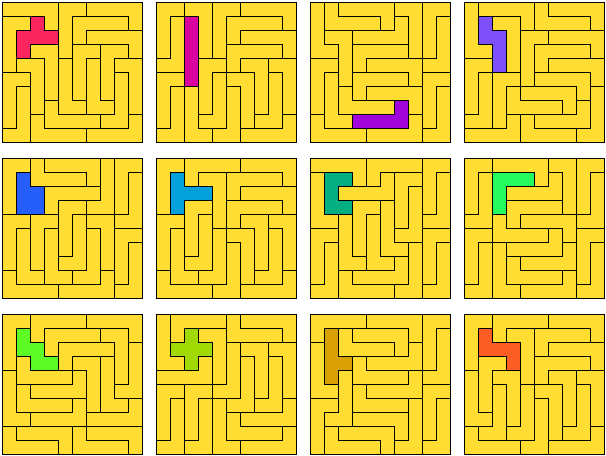
Aad van de Wetering verbeterde sommige resultaten met de P-pentomino
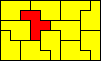 10x6 (AW) |
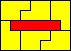 7x5 (AW) |
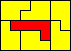 7x5 (AW) |
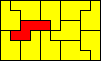 10x6 (AW) |
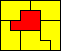 6x5 (AW) |
 7x5 (AW) |
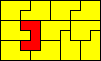 10x6 (AW) |
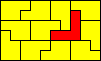 10x6 (AW) |
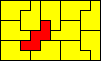 10x6 (AW) |
 5x5 (AW) |
 7x5 (AW) |
 7x5 (AW) |
Van George Sicherman kregen we voor een
variant van dit probleem de volgende
oplossing toegestuurd.
De afmetingen van de rechoek zijn 10 en 6.
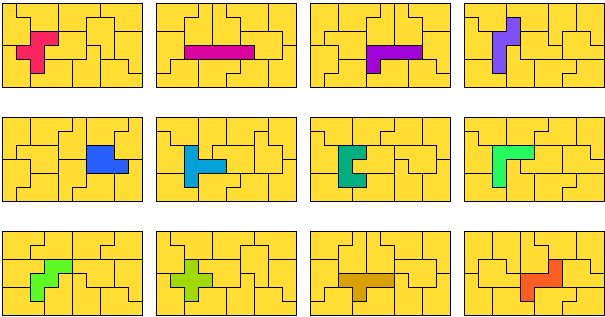
Aad van de Wetering
(AW) vond ook alle
oplossingen met de Y-pentomino. George Sicherman (GS) verbeterde sommige
resultaten.
 5x5 (AW) |
 15x6 (GS) |
 10x5 (AW) |
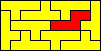 10x5 (AW) |
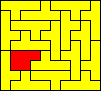 10x9 (AW) |
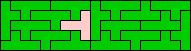 19x5 (GS) |
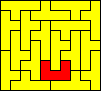 10x9 (AW) |
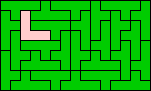 15x9 (GS) |
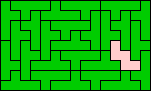 15x9 (GS) |
 5x5 (AW) |
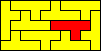 10x5 (AW) |
 5x5 (AW) |
Van George Sicherman kregen we voor een
variant van dit probleem de volgende
oplossing toegestuurd.
De afmetingen van de rechthoek zijn 20 en
10.
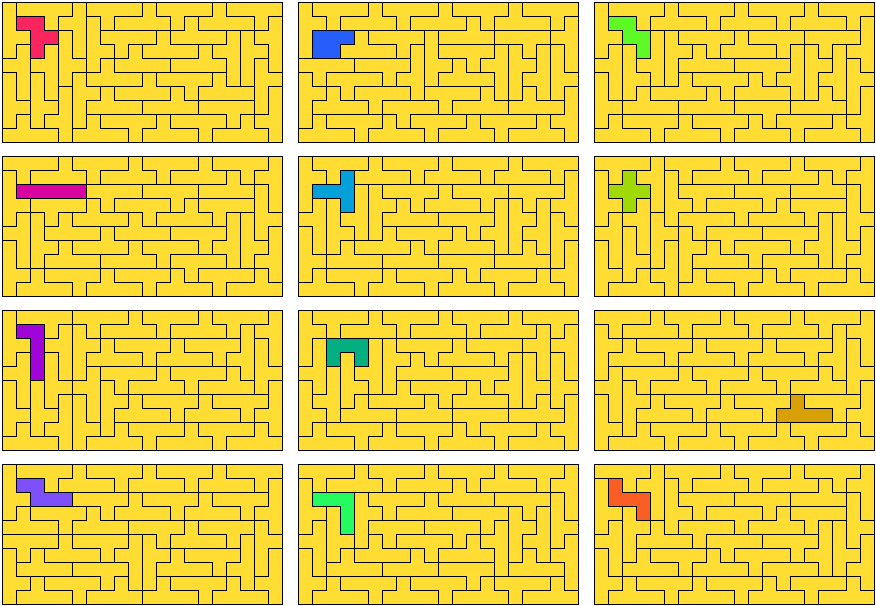
Na het krijgen van de
oplossingen van George met de F-pentomino hebben we de opgave geplaatst. We
gaan niet echt akkoord dat de pentomino's een rechthoek vormen maar vinden
het toch schitterend gevonden.
We plaatsen telkens de maten van de omgeschreven rechthoek.
 11√2 x 10√2 (GS) |
 10√2 x 6√2 (GS) |

11√2 x 10√2 (GS) |
 11√2 x 10√2 (GS) |
 11√2 x 10√2 (GS) |
 11√2 x 10√2 (GS) |
 10√2 x 6√2 (GS) |
 10√2 x 6√2 (GS) |
|
|
|
|
|
Van Livio Zucca kregen we voor een
variant van dit probleem deze leuke oplossing toegestuurd.
De zijde van het omgeschreven vierkant is
12√2

George Sicherman (GS) mailde: "Can you make room for a few more?"
Met veel plezier!
We plaatsen telkens de maten van de omgeschreven rechthoek.
 (32√5):5 en (22√5):5 (GS) |
 (27√5):5 en (27√5):5 (GS) |

(37√5):5 en (22√5):5 (GS) |
 (22√5):5 en (22√5):5 (GS) |
 (32√5):5 en (22√5):5 (GS) |
 (42√5):5 en (22√5):5 (GS) |
 (27√5):5 en (27√5):5 (GS) |
 (37√5):5 en (27√5):5 (GS) |
|
|
|
|
|
Van George Sicherman kregen we voor een
variant van dit probleem de volgende
oplossing toegestuurd.
De afmetingen van de omgeschreven
rechthoek zijn
(37√5):5 en (32√5):5
.
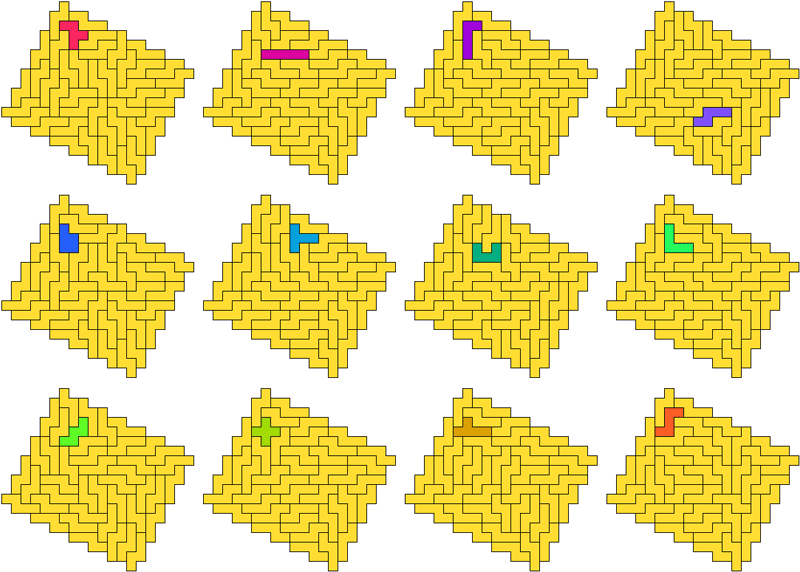
George mailde als antwoord: "And here are some more tricks with W!"
We plaatsen telkens de maten van de omgeschreven rechthoek.
 7√2 x 7√2 (GS) |
 11√2 x 10√2 (GS) |

9√2 x 9√2 (GS) |
 9√2 x 9√2 (GS) |
 9√2 x 9√2 (GS) |
 9√2 x 9√2 (GS) |
 11√2 x 10√2 (GS) |
 11√2 x 10√2 (GS) |
|
|
|
|
|
Van George Sicherman kregen we voor een
variant van dit probleem de volgende
oplossing toegestuurd.
De maten van de omgeschreven rechthoek zijn
11√2x
10√2.

George vond er nog eentje: "Here is one more "trick rectangle"
De zijde van het omgeschreven vierkant is (17√5):5

(GS)
Eigenlijk was dit ons
potpourri-probleem 25 dat we kregen van Toshi Kato uit Japan:"Hoeveel
X-pentomino's kan je leggen in een vierkant van 8x8?"
Andere of betere oplossingen gevonden?
![]()
![]()











