Omsluiting met symmetrie-as

Aad Thoen stuurde een mail met de volgende uitdaging:
Maak een zo groot mogelijke symmetrische (zowel binnen als buiten) omsluiting met een diagonale symmetrie-as.
Hier een voorbeeld met 7 pentokes en omsluiting van 31.

We breiden echter de uitdaging uit tot een omsluiting met een symmetrie-as.

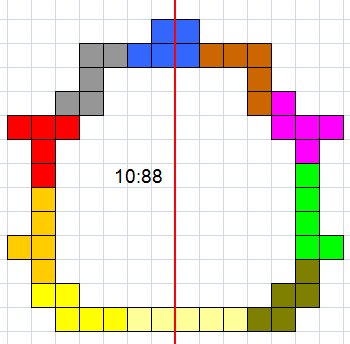
Aad heeft met 11 pentokes 85 ingesloten vakjes. De figuur is wat ingekleurd om de diagonale symmetrie beter zichtbaar te maken.

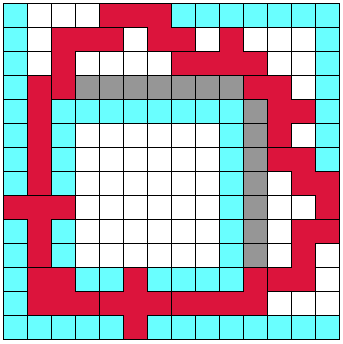
Aad heeft ook oplossingen met omsluitingen van 48, 51 en 54. De doorbraak naar 85 kwam toen hij vond hoe T en X met elkaar te laten corresponderen.
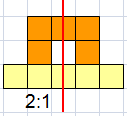
Met 2 pentomino's hebben we 1 vakje ingesloten.


(HP)


(HP)

Alle mogelijke figuren bestaande uit 2 verschillende pentomino's die een symmetrieas hebben staan op een andere pagina op deze site.

Met 3 pentomino's .

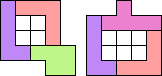
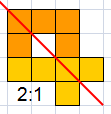
George Sicherman:"I think I set the record for four pentominoes with a diagonally symmetric!"

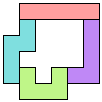
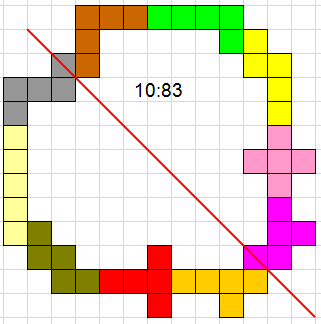
Er zijn 11 vakjes ingesloten.

We laten echter ook orthogonale symmetrie toe als er maar een symmetrie-as is !


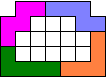
Met 5 pentomino's


23 (OM en HP)


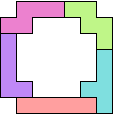
21 (GS en HP)

Met 6 pentomino's


Aad Van de Wetering
(en HP)


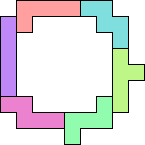
ILNWYZ
32(GS en HP)


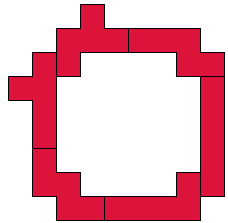
FILNWY
32(AT)

Met 7 pentomino's


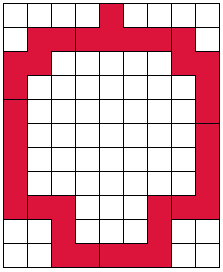
46 (AT)


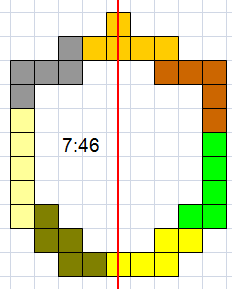
Helmut Postl


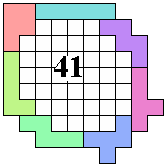
George Sicherman


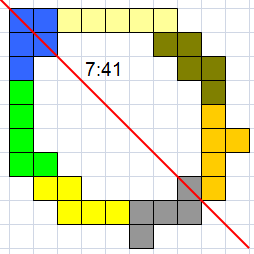
Helmut Postl

Met 8 pentomino's


Aad van de Wetering


Helmut Postl


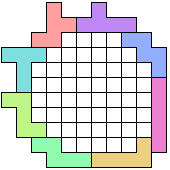
54(OM)


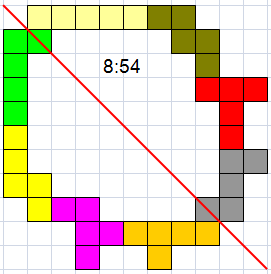
Helmut Postl

Met 9 pentomino's


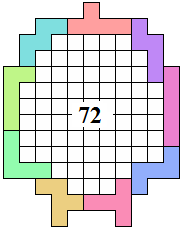
George Sicherman


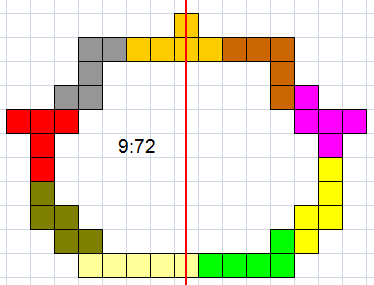
Helmut Postl


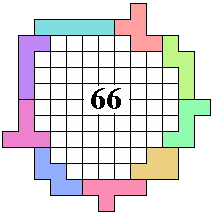
George Sicherman


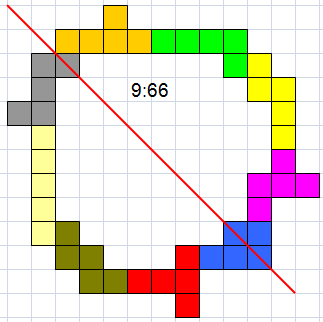
Helmut Postl

Met 10 pentomino's
Aad Thoen: "Dankzij de FT combinatie van GS doe ik weer even mee." Dit is de reden waarom George zijn oplossing er nog staat.


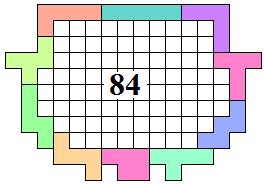
George Sicherman


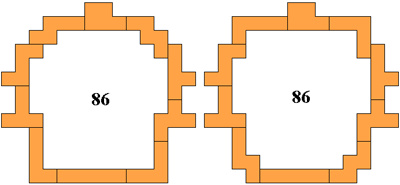
Aad Thoen

Maar dan komt Helmut

Met 11 pentomino's


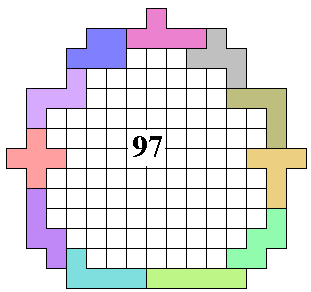
(OM, AW en HP)


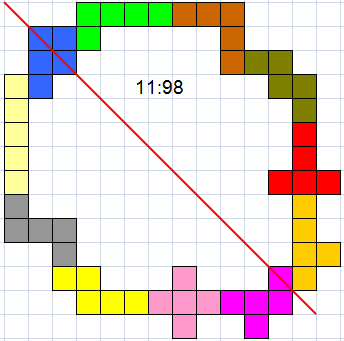
Helmut Postl

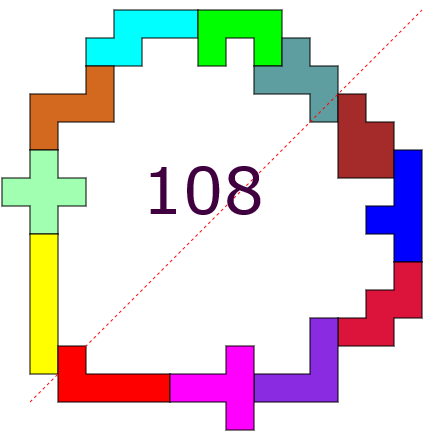
Met 12 pentomino's
Hieronder de 3 laatste resultaten
 


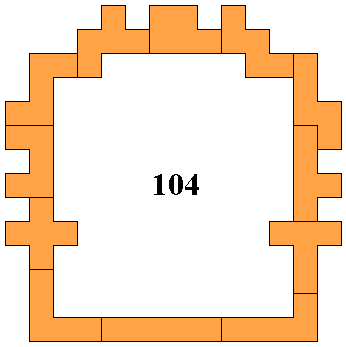
Aad Thoen


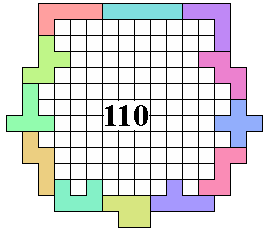
George Sicherman


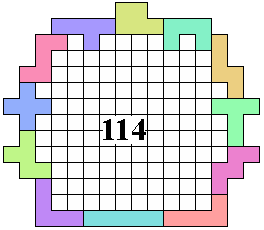
Odette De Meulemeester
(gevonden 2016)

Van Rodolfo Kurchan kregen we een foto van het voorblad van Puzzle Fun van april 1995.

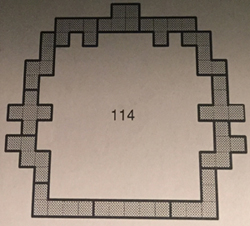
Dit record staat schijnbaar op naam van Mike Reid.
L'histoire se répète (voor de insiders en onze kubusman ;-)
Onze oplossing is niet volledig dezelfde en we zijn blij met de gevonden resultaat.
Helmut Postl vond ook 114 maar op een andere manier:

 

 
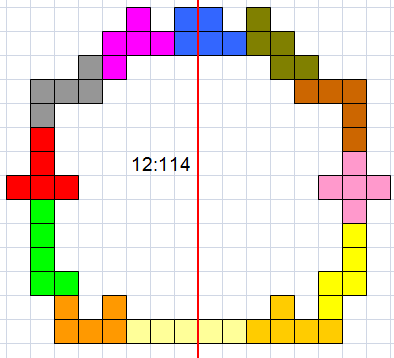
Aad van de Wetering


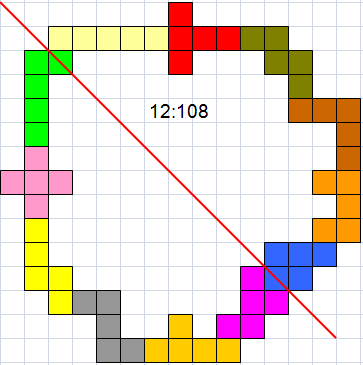
Helmut Postl

Met deze set zoekt Aad van de Wetering al zijn records

We zijn op zoek naar zo'n magische set ;-)

Hieronder nog enkele omsluitingen die uit verschillende delen bestaan.


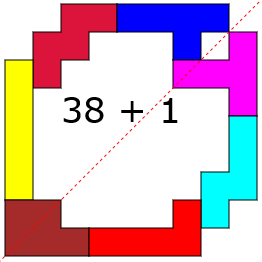
+1 is discutabel
 Dat extra vakje ligt zeker en vast binnen de buitenomtrek. Ook buiten de binnenomtrek, maar wie maalt daarom....
 38+1=38(AW)  


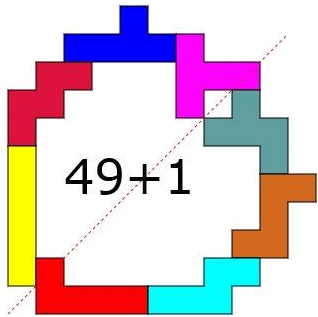
(AW)


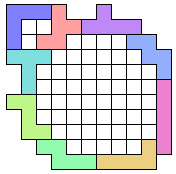
(OM)



Edo Timmermans had reeds vroeger (ter gelegenheid van wedstrijd 51) een omsluiting met symmetrie-as zowel voor binnen- als buitenomtrek met alle pentomino's toegestuurd.

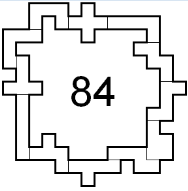
Hij stuurde ook omheiningen met 8 pentomino's die de ontvouwing zijn van een leeg doosje.

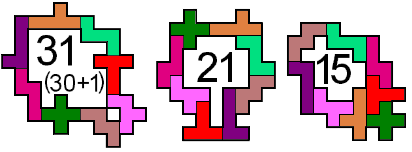
Edo zocht ook omheiningen met de hexomino's die de ontvouwing zijn van een kubus.


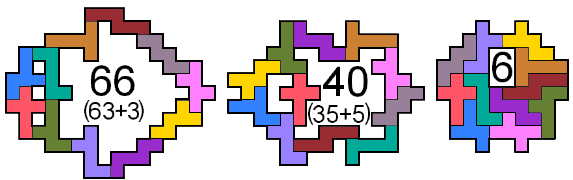
Andere omsluitingen met een symmetrie-as gevonden?
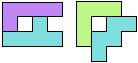
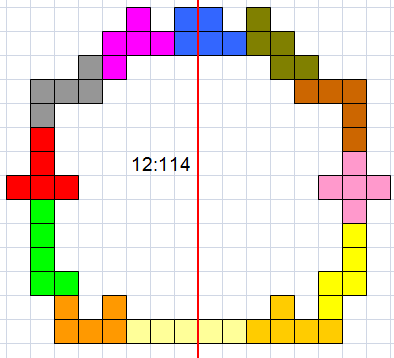
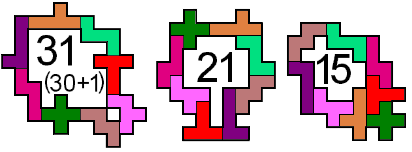
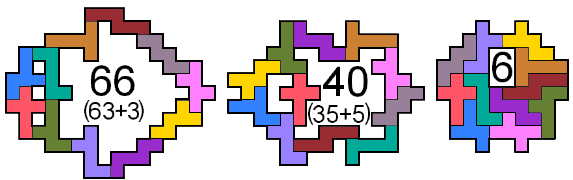