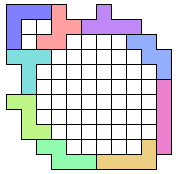
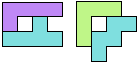Aad Thoen sent me an e-mail with the following challenge:
Make a as large as possible symmetrical (inside as well as outside) enclosure with a diagonal axis of symmetry.
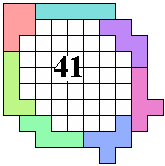
Here an example with 7 pentominoes and enclosure of 31.
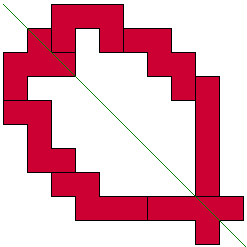
However we extend the challenge to enclosures with any axis of symmetry (diagonal or orthogonal).
Aad has enclosed 85 units with 11 pentominoes. Colors have been added to the figure to make the diagonal symmetry more visible.
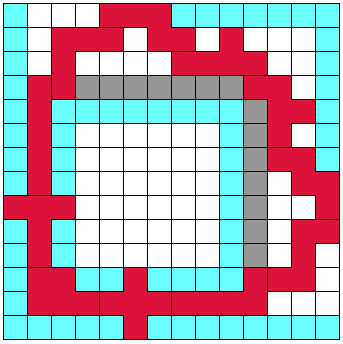
Aad found also solutions with enclosures of 48, 51 and 54. The breakthrough to 85 came when he discovered how to let T and X correspond.
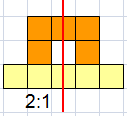
With 2 pentominoes we have enclosed 1 unit.
|
|
|
|
All
possible figures consisting of 2 different pentominoes with an axis of
symmetry are contained in
another page
of this site.
With 3 pentominoes .
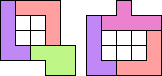
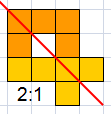
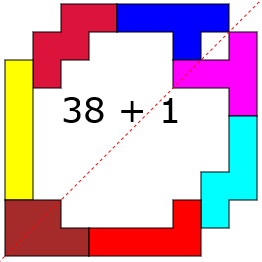
George Sicherman:"I think I set the record for four pentominoes with a
diagonally symmetric!"
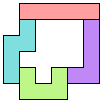
11
units are enclosed.
We
also admit orthogonal symmetry, as long as any axis of symmetry is present!
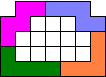
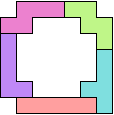
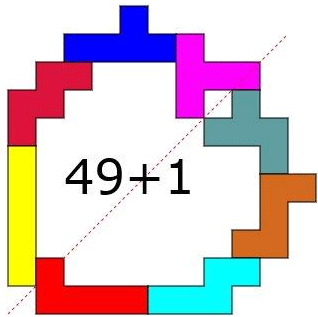
With 5
pentominoes
|
|
|
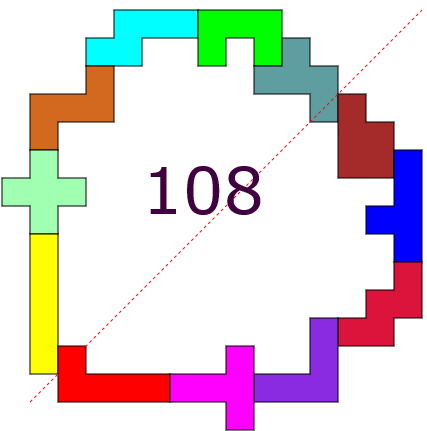
With 6 pentominoes
With 7 pentominoes
With 8 pentominoes
With 9 pentominoes
With 10 pentominoes
But here is Helmut!
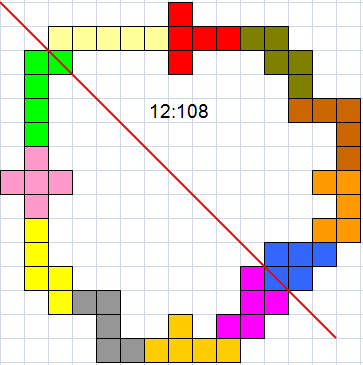
With 11 pentominoes
With 12 pentominoes

Aad Van de Wetering
(and HP)
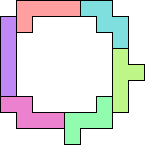
ILNWYZ
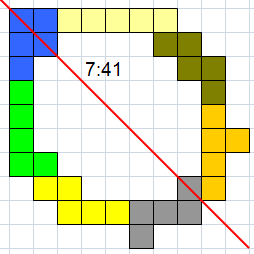
32(GS)
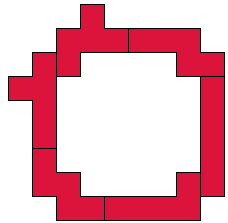
FILNWY
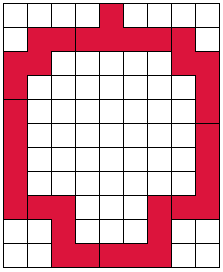
32(AT)
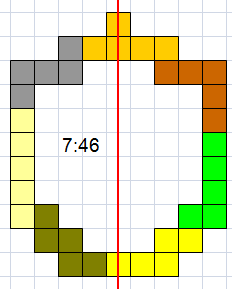
46 (AT)
Helmut Postl
George Sicherman
Helmut Postl

Aad van de Wetering

Helmut Postl
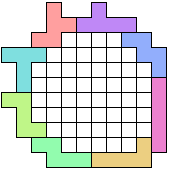
54(OM)
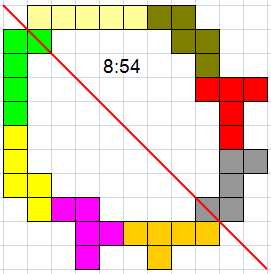
Helmut Postl
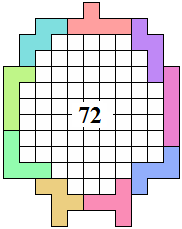
George Sicherman
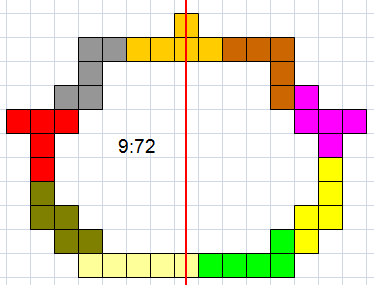
Helmut Postl
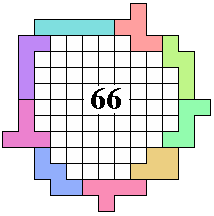
George Sicherman
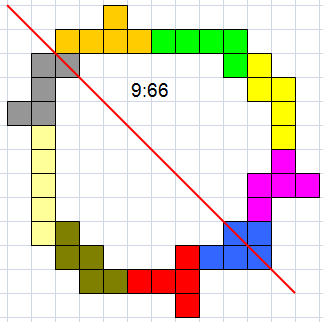
Helmut Postl
Aad Thoen:
"Thanks to the FT combination of GS I join the game again."
This is why the solution of George is still present.
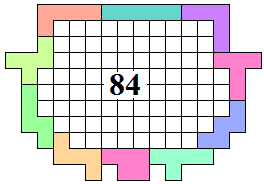
George Sicherman
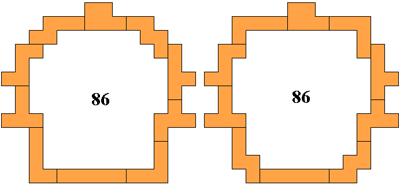
Aad Thoen
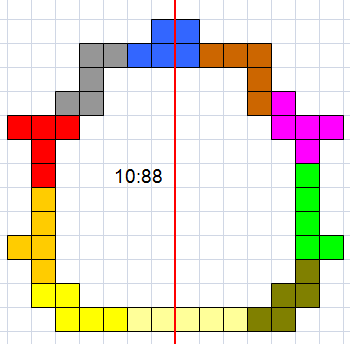
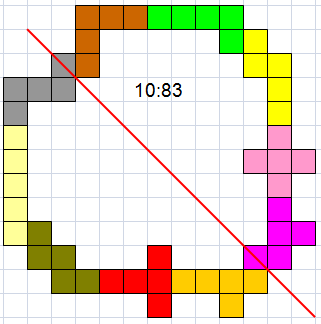
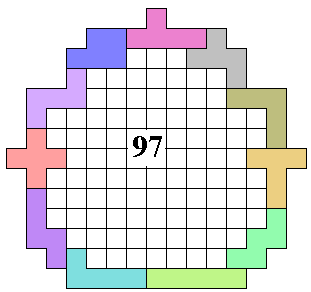
(OM, AW and HP)
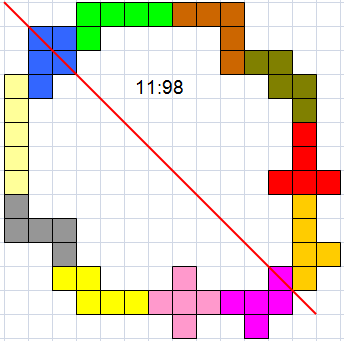
Helmut Postl
The 3 latest results follow:
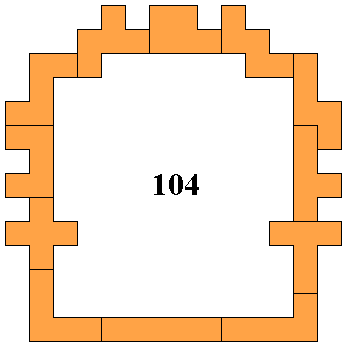
Aad Thoen
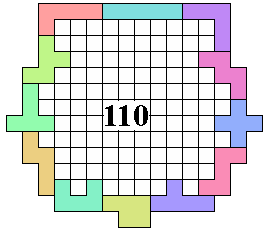
George Sicherman
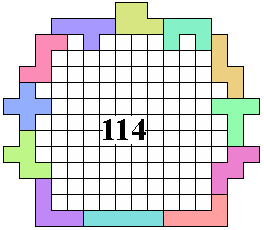
Odette De Meulemeester
(found 2016)
From Rodolfo Kurchan we got a picture of the front cover of Puzzle
Fun of April 1995.
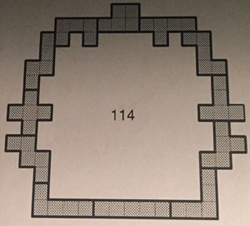
This record apparently is on the credit of Mike Reid.
L'histoire se répète (for insiders and our
kubusman
;-)
Our solution is not completely identical and we are thrilled with
the finding.
Helmut
Postl also found 114 but in a different way:
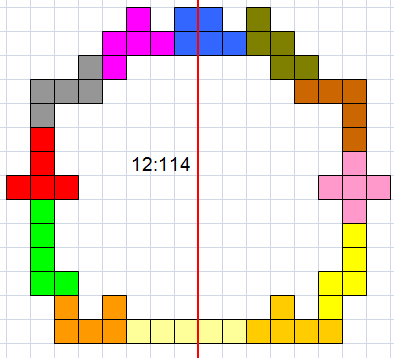
|
Aad van de Wetering |
|
With this set Aad van de Wetering searches for all his records

We are looking for such a magical set ;-)
|
|
|
|
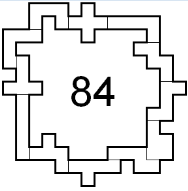
Edo Timmermans had already earlier (on the occasion of contest 51)
sent an enclosure symmetrical on the in- and outside with all
pentominoes.
He also sent fencings with 8 pentominoes which are the enfolding of
an empty box.
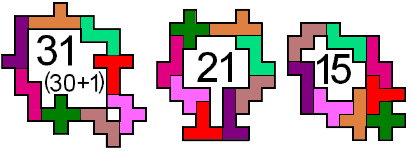
Edo further searched for fencings with the hexominoes which are the
enfolding of a cube.
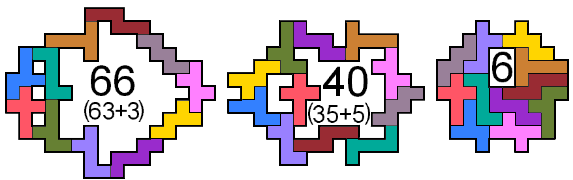
Did you find any other enclosures with an axis of symmetry?
![]()
![]()